☰

3. Modelling learning path

Causal modelling: Quantum particle in a box

The pre-university physics examination programme (vwo) includes the new domain Quantum World.1 This world is populated by a large number of models: the Bohr model of the atom, the photon model of light, the quantum model of a particle, and so on. These models have a solid foundation in natural sciences, but at the first introduction to these models they are abstract and weird.

As a simple model, a particle is considered in a one-dimensional box.2 The learning goal is that students can explain on the basis of this model that quantisation is the result of confinement of particles, such as electrons, and that with the help of quantum mechanics spectra of atoms and molecules can be calculated in detail.

potentiaalput

Fig 3.3 Wavelengths in a 1D box

energieniveaus

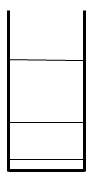
Fig 3.4 Energy levels in a 1D box

The question is which wave functions match a particle in a one-dimensional box. This can be calculated with a few rules:

  1. For a particle of mass m there exists a fundamental relationship between the wavelength and the particle property ‘momentum’. This relation was determined by Louis de Broglie in 1924:
    λ B = h p = h m⋅v The defined wavelength λB is called the 'de Broglie wavelength'. When a particle is in such situation that the de Broglie wavelength may play a role one speaks of a 'quantum particle'.

  2. Suppose a quantum particle is inside a one-dimensional box (i.e, inside a infinitely deep potential well). At the boundaries of the box and beyond, the quantum particle cannot be found. There the wave function is zero.  The first possible solution is one that has half a wavelength fits the width of the box. For a box of width L, the de Broglie wavelength equals 2L:
    λ B = h m·v =2L
  3. More generally, an integral number of half the wavelength must fit the width of the box:
    λ n =  2L n , with n=1,2,3,…. Other waves are not equal to zero at the boundaries and are therefore not permitted. Students can calculate the corresponding energy levels of the quantum particle and make a sketch of the energy spectrum.

The model of a quantum particle in a box is an example of a causal model. Although strongly simplified, the model makes it plausible that emission and absorption spectra of atoms are quantised and that these spectra can be calculated from transitions of electrons between energy levels.3