Computeralgebra-systemen

De eerste systemen die werden ontwikkeld in de zestiger jaren waren met name gericht op het uitvoeren van zeer grote berekeningen, die voortkwamen uit specifieke terreinen van de natuurkunde. Vanwege die specifieke gerichtheid noemen we dit soort systemen ``special purpose systems''. Voorbeelden hiervan zijn CAMAL (hemelmechanica), SHEEP (relativiteitstheorie) en Schoonschip (hoge energie fysica). Ook de eerste versie van REDUCE is in die tijd ontwikkeld door A. Hearn als ``special purpose system'' voor berekeningen aan Feynman-diagrammen, een onderwerp uit de hoge energie fysica.

De ontwikkeling van special purpose systemen heeft sindsdien niet meer stilgestaan. Voorbeelden van na 1985 zijn GAP en Cayley (groepentheorie), PARI, SIMATH, KASH en LiDIA (getaltheorie), Macaulay en Singular (algebraische meetkunde), CoCoA (commutative algebra), LiE (Lietheorie), en nog veel meer.

Met een vereenvoudiging van de historie kunnen we drie golven van computeralgebra-systemen onderkennen. Na de eerste golf van special purpose systemen, en met de mogelijkheden als hierboven geschetst, komt er een golf van ``general purpose systemen''. Deze systemen voorzien hun gebruikers van een rijk arsenaal aan datastructuren en wiskundige functies, daarmee proberend zoveel mogelijk verschillende computationele gebieden te bestrijken. Een general purpose systeem wordt daarom wel eens vergeleken met Zwitsers zakmes: voor elke klus wordt gereedschap geboden. En mocht dit nog niet toereikend zijn, dan kan een gebruiker een general purpose systeem in bijna alle gevallen als programmeertaal gebruiken om gewenste algoritmen in te implementeren.

We geven een lijstje met namen en een korte beschrijving van de belangrijkste general purpose systemen in volgorde van beschikbaarstelling (waarbij gezegd dat alle genoemde systemen nog verder ontwikkeld worden en regelmatig in nieuwe versies uitkomen). Voor een uitgebreid overzicht van computeralgebra-systemen, zie [1], of raadpleeg het electronische informatiesysteem CAIN (www.can.nl).

REDUCE

is van origine bestemd voor hoge energie fysica. Echter bleek het al snel ook daarbuiten bruikbaar te zijn. Het biedt een programmeertaal met twee modi: ``algebraic mode'' en ``LISP mode''. Met name de tweede maakt dat REDUCE een zeer open systeem is en dat zeer efficiënt en flexibel aan de wensen van een gebruiker aan te passen is. Het heeft een uitgebreide bibliotheek van programma's en functies, waaronder faciliteiten voor het genereren van Fortran en C-code. De gebruikersinterface doet wat ouderwets aan, mede door het ontbreken van grafische mogelijkheden.

Macsyma

verscheen in 1971. Het is gebaseerd op LISP en ontwikkeld op M.I.T. Het heeft een uitgebreide bibliotheek van functies, en algoritmen. Macsyma kan de gebruiker vragen stellen als het meer gegevens nodig heeft voor het bepalen van een antwoord (zie het voorbeeld verderop). In 1992 is het na jaren van stilte een tweede leven begonnen: een versie voor MS-Windows is gelanceerd door een nieuw bedrijf, Macsyma Inc.

Maple

is ontstaan uit het ``Maple Project'' uit de beginjaren '80 met o.a. G. Gonnet en K. Geddes aan de Universiteit van Waterloo (Canada). In 1992 is er een bedrijf, Waterloo Maple Software, voor de commercialisatie opgericht. Maple is ontworpen met een kleine kern geschreven in C, die de basale operaties uitvoert. De meeste wiskundige functies zijn geschreven in de taal Maple, en deze Maple-code is toegankelijk voor de gebruiker.

Mathematica

is het tweede systeem dat door S. Wolfram is ontworpen. Het eerste, SMP, heeft veel overeenkomsten met het symbolische deel van Mathematica, maar is nooit echt aangeslagen. Van Mathematica kan dit niet gezegd worden: het zonder twijfel het meest gebruikte computeralgebra-systeem, waarover de meeste boeken en artikelen verschenen zijn, en waarvoor door gebruikers de meeste code aangeleverd wordt op de Web-site http://www.mathsource.com. Voor dit succes zijn diverse redenen aan te voeren. Bij de introductie in 1988 van Mathematica stonden twee zaken voorop: een goede integratie van symbolische, numerieke en grafische mogelijkheden, en een goede marketing. Met Mathematica kunnen ``notebook''-documenten gemaakt worden, waarin op natuurlijke wijze tekst, grafieken, invoer en uitvoer gentegreerd zijn. Deze aanpak was nieuw in de wereld van computeralgebraci en zette de deur voor gebruik van computeralgebra door niet-ingewijden wijd open.

Derive

is ontwikkeld door D. Stoutemyer en A. Rich, en in 1988 als opvolger van MuMath (uit 1980) op de markt gebracht. Opmerkelijk in vergelijking met de andere systemen is de beperkte omvang van het pakket, en het gemak waarmee een gebruiker via menu's aan de slag kan. Derive is op dit moment alleen voor het MS-DOS platform beschikbaar, een Windows versie is in de maak. De programmeertaal van Derive biedt evenwel een bescheiden functionaliteit.

FORM

is een pakket dat speciaal ontworpen is om met gigantisch grote formules efficiënt te kunnen manipuleren. Denk hierbij aan formules die niet niet in hun geheel in het werkgeheugen van de computer passen. Dit beperkt de mogelijke wiskundige instructies aanzienlijk; verwacht geen factorisaties van veeltermen en dergelijke. Toch is FORM niet alleen in het vakgebied waarvoor het primair ontwikkeld is, nl. hoge energie fysica, de kraker van grote formules.

MuPAD

is een pakket dat qua werking op Maple lijkt maar minder wiskunde ingebouwd heeft. Daar staat tegenover dat het ontworpen is voor parallel rekenen, dat je algoritmen voor algemene rekendomeinen (bv. ringen) kunt definiëren, en dat het voor niet-commercieel gebruik gratis beschikbaar gesteld wordt.

Magma

is de opvolger van Cayley, maar is qua functionaliteit uitgegroeid tot een general purpose programma rondom de algebraische begrippen van structuren (groepen, ringen, modulen, designs, codes, grafen, etc.) en morfismen. Het doel van de makers aan de Universiteit van Sidney is om berekeningen in algebra, getaltheorie, meetkunde, algebraische combinatoriek, groepentheorie, e.d. te ondersteunen.

Axiom

is de naam die NAG in 1992 gegeven heeft aan het pakket dat onder de naam Scratchpad door een onderzoeksteam bij IBM Yorktown Heights is ontwikkeld. In tegenstelling tot de andere pakketten werkt de object-georiënteerde programmeertaal met ``typen'', zoals Integer en UnivariatePolynomial. Hiermee is het mogelijk om goed met mathematisch structureren te werken, en biedt dit systeem veel mogelijkheden voor werkelijke computeralgebra en niet alleen symbolisch manipuleren met bits-and-bytes. Er zijn voortreffelijke grafische faciliteiten in Axiom, een Hypercard-gebaseerd hulpsysteem en men vindt er de beste implementaties van het Gröbner algoritme en het Risch algoritme. Ten nadele van Axiom spreekt de omvang van het pakket en de overhead die het type-systeem met zich meebrengt.

Al deze systemen bieden behalve wiskundige functies, ook een programmeertaal. Zo'n taal kunnen we zien als een high level mathematics programming language. Programmeren in een dergelijke taal is vaak relatief eenvoudig, veel programma's bestaan slechts uit één regel. Bijvoorbeeld, in Mathematica kunnen op de volgende manier honderd random floating-point getallen uniform gedistribueerd in het interval gemaakt worden en beginned bij 0 cumulatief opgeteld worden:

In[1]:= FoldList[Plus, 0, Table[Random[Real,{-1,1}],{100}]];

In[2]:= ListPlot[%, PlotJoined->True];

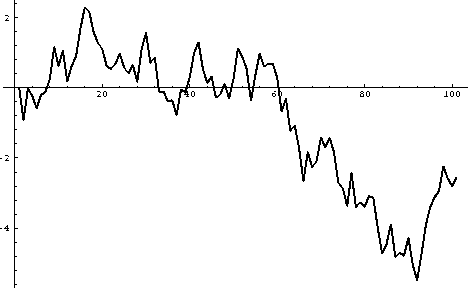
Echter kan efficiëntie wel eens tegen vallen, als het vergeleken wordt met een taal op een lager niveau, zoals C of FORTRAN. Voordeel van pakketen zoals Axiom, Maple en Mathematica is wel dat allerlei programmeerstijlen (procedureel, functioneel, regelgebaseeerd, object-georiënteerd) binnen één omgeving aanwezig zijn. Je kunt dus veelal dié stijl kiezen die het best past bij het wiskundig probleem of waarin je het beste thuis bent.

Ter illustratie van verschillende programmeerstijlen in één computeralgebra-systeem laten we verschillende Mathematica manieren zien om gegeven een lijst en gegeven een element alle plekken waar dit element in de lijst voor komt te verwijderen.

regelgebaseerd (iteratief)

In[3]:= removeAll1[list_, elt_] := 
           list //. removeRule[elt]
In[4]:= removeRule[elt_] := {b___, elt, e___} -> {b, e}
In[5]:= removeAll1[{x, a, b, x, c}, x]

Out[5]= {a, b, c}

regelgebaseerd (recursief)

In[6]:= removeAll2[{}, elt_] := {}
In[7]:= removeAll2[{elt_, rest___}, elt_] :=
            removeAll2[{rest}, elt]
In[8]:= removeAll2[{other_, rest___}, elt_]:=
            Prepend[
                    removeAll2[{rest}, elt],
                    other
            ]
In[9]:= removeAll2[{x, a, b, x, c}, x]

Out[9]= {a, b, c}

functioneel

In[10]:= removeAll3[list_, elt_] :=
            Select[list, Function[x,x=!=elt]]
In[11]:= removeAll3[{x, a, b, x, c}, x]

Out[11]= {a, b, c}

procedureel

In[12]:= removeAll4[list_, elt_] :=
         (templist = {};
          Do[
            If[
                   list[[i]]=!=elt,
                   AppendTo[templist, list[[i]]]
            ],
            {i, 1, Length[list]}
          ];
          templist
          )
In[13]:= removeAll4[{x, a, b, x, c}, x]

Out[13]= {a, b, c}

Ingebouwde routines

In[14]:= Flatten[{x, a, b, x, c} /. x->{}]

Out[14]= {a, b, c}

Geen wonder dat computeralgebra-systemen ook veel ingezet worden voor het snel maken van prototypes van computercode en voor het snel uittesten van nieuwe algoritmen.