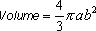
The main reasons to prefer approximations of the egg curve with semi-ellipses of which the mathematical formulas are in canonical form are:
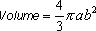
and

with eccentricity e given by
 .
.The major perimeter of the surface of revolution is given by:
 ,
,
where E is the complete elliptic integral of the second kind. These formulas can be found on Internet (e.g. http://mathworld.wolfram.com/Perimeter.html) and I do not expect that many a student is able to derive the formulas or even knows what an elliptic integral actually is. However, in principle, the formulas can be computed via integration:
 ,
,
 ,
,
and
 ,
,
where
 .
.With the exception of volume, and then only in case of a simple function f, you may need a computer algebra system to find the correct mathematical expressions for the integrals. This is not a serious problem because useful approximations of the perimeter of an ellipse exist and can be applied (e.g., see Final Answers). The following approximation of the perimeter of an ellipse originates from the great mathematician Ramanujan (1913-1914):
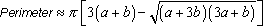
The following combination of arithmetic and geometric mean (Bronshtein & Semendyaev, 1985) is also very attractive to use in an egg investigation:
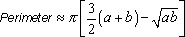
When the above formulas are applied to the approximation of the egg curve by two semi-ellipses with parameters as = 2.75 (small ellipse), ab = 3.43 (big ellipse) and b = 2.30 (both ellipses), then one gets a volume of 68.5 ml, an area of 82.2 cm2, a minor perimeter of 14.5 cm and a major perimeter of 17.0 cm. The computed volume and surface area are in agreement with the measured quantities. The computed area is in agreement with the estimated value according to the following allometric power-law between weight (in gram) and area of avian eggs (in cm2) (Paganelli et al, 1974):
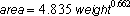
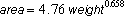
This gives the following value of surface area: 81.7 cm2. My computer values are between these two estimates. By the way, there also exist experimentally found relationships between the volume and area of an egg. For example (Hoyt, 1976):
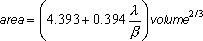
If you fill out the measured volume of 68 ml, then the estimated surface area is also 81.7 cm2. In summary, the above surface area computation and the allometric laws found in the literature are in good agreement.
The equation for the volume V of an egg can also be written as
 ,
,
where λ = as + ab and β = 2b represent the length and width of the egg, respectively. This formula for the volume can be used to estimate the thickness of the eggshell as a root of a polynomial. I outline the method after (Narushin, 1998):
To my purpose, an egg consists of two components: the shell and the contents of the egg. The mass m of the egg is the sum of the mass ms of the eggshell and the mass mc of the egg’s contents. Let V, Vs and Vc be the volumes of the complete egg, of the shell only, and of the contents only, respectively. Let ρs and ρc be the density of the shell and the contents of the egg, respectively. It holds:
and
Rewriting leads to the following expression for the volume of the contents of the egg:
 .
.
Assume that the complete egg can be approximated as a surface of revolution of two semi-ellipses with canonical parameters as, ab and b. The same assumption can be made for the contents of the egg, but in this case with the canonical parameters
As = as - δ, Ab = ab - δ and B = b - δ.
So, the existence of an air cell in the egg and the variation in shell thickness, which depends on the particular spot on the egg, are neglected. The formula for the volume of the contents of the egg is:
 .
.
Working out leads to:
 .
.
Rewriting in terms of length λ and width β of the egg leads to:
 .
.
Thus the eggshell thickness δ must satisfy the following third degree polynomial equation:
 .
.
In the standard work (Romanoff & Romanoff, 1947) you can find the required densities for shell and contents of avian eggs: ρs = 2.3 g/cm3 and ρc = 1.037 g/cm3. Other data of the hen’s egg under consideration are: m = 74 g, V = 68 cm3, λ = 6.21 cm, and β = 4.62 cm. The shell thickness δ of the hen's egg under consideration in this article must satisfy the following polynomial equation:
δ3 − 7.725δ2 + 19.6812δ − 0.6585 = 0.
The only real solution is δ = 0.034 cm. This is 2.5 μm less than the thickness according to the following allometric law (Ar et al, 1974):
δ = 5.126·10-3 · weight0.456.
Quite a nice result of the mathematical modeling of the hen's egg.