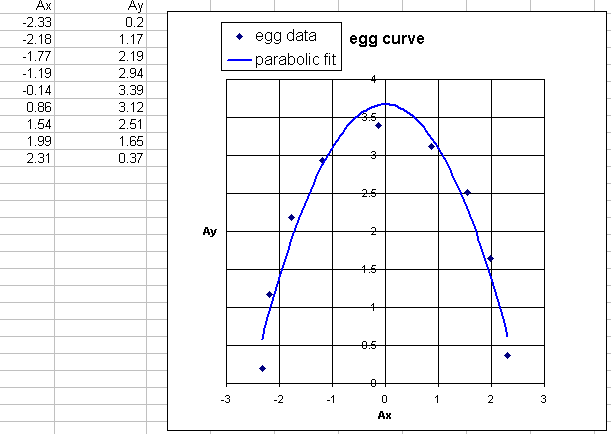
Figure 7. Screen shot of an Excel sheet illustrating a parabola as regression curve.
Regression is a third technique to find a suitable egg curve. All you have to do is to find in a GeoGebra activity the coordinates of points on the rim of the egg in the digital image (see Figure 6) and copy the coordinates found to a spreadsheet program such as Excel or another program that offers the possibility to compute a quadratic regression curve for data points.
Figure 6. Collecting data points.
Figure 7 is a screen shot of an Excel data sheet in which the quadratic fit
of the measured data points has been determined via the chart menu item Chart / add Trendline,
where the choice for a second degree polynomial is made. Notice that the parabola does not match very well with the data
points, which is confirmed when the accuracy of the proposed least-squares approximation is determined in the usual
numerical way of computing the standard deviation or by using another quality-of-fit criterion.
Only by taking smaller parts of the data set, a polynomial fit will lead to a suitable description
of the selected part of the hen's egg curve.
Figure 7. Screen shot of an Excel sheet illustrating a parabola as regression curve.

By the way, the profile of an egg of a marbled godwit can be modeled decently with a parabola and an ellipse (see Figure 8).
Figure 8. An approximation of a marbled godwit egg with a parabola and an ellipse.
You can replay or step through the above algebraic construction, or you can even give it a try yourself after rewinding the construction to its beginning. You can always reset the construction to its original state by pressing the reset icon in the upper right corner of the drawing pad.