Started Labbook 2026.
The Master version of this course will be Vision for Autonomous Robots, so the rest of the development can be followed on this labbook.
December 10, 2025
- Another nice system to build on, because it is well maintained (says Sebastian), is LeRobot SO-101.
- Sebastian also made a path-planning testing tool: PyRoboSim.
- Sebastian also has an experimental path-planner: RoboPlan.
December 9, 2025
- There is a new book (March 2024) of Artificial Intelligence for Robotics. According to The Construct to quickly apply ML techniques, not for rigorous academic foundation.
- The code on github is 7 years old, so is based on ROS1 Kinetic.
- Checked the figures of the book, it is based on a small mobile robot (Raspberri Pi controlled), with a simple arm, which picks up toys from the ground (recognized with a CNN) and at the end gets a personallity (Embodied AI!)
- The ROS2 code of the 2nd edition is also on github.
- The code for Chapter1 looked still the same ROS1, but Chapter 4 is clearly ROS2.
- The robot now also received a major update. Omnidirectional wheels, Nvidia Jetson Nano as controller:
Augustus 21, 2025
June 23, 2025
- Via the new textbook Robotics Goes MOOC - Knowledge I enrolled in the corresponding MOOC is hosted by Federica.eu.
- There are actually two MOOCs, the first MOOC (Robotics in a Nutshell) covers the first chapters of AMR:
- The Journey of Robotics
- Sensing and Estimation
- Force Control
- Knowledge Representation and Reasoning
In total of 11 weeks, including Graping and Manipulation. Only quizes, no assignments.
The videolectures are Prof. Bruno Siciliano interviewing Prof. Oussama Khatib, the author of the first chapter.
The first videolecture ends with the Perception-Thinking-Action cycle.
The history of first part of20-century is rather short: Čapek's play R.U.R. and Isaac Asimov's Three Laws.
The second part of the 20-century is summarized in a 7 minute video from the Handbook, the ICRA 2000 50y of celebration.
The towards video is also from the Handbook
The Odometry Unit is video lecture is presented by Andreas Nüchter, one of the authors of the 2nd chapter Sensing and Estimation.
That chapter starts quite brief, but is quite extensive on 3D lasers and triangulation. Therefore not a bad choice for AMR or VAR.
March 18, 2025
- Checked Linux, Wintel and WWW for old material, should also try at home.
March 11, 2025
- Looking around for a more details on the sigma-points.
- Instead, found a nice SLAM lecture (2016) from Raquel Urtasun. CSC 2541 stands for topics in Machine Learning, so the topic chnages every year. This are their list of Robotics courses. Most interesting is Computer Vision for Robotics.
March 5, 2025
- Watched the Refresher on Probability Theory, the only lecture of Localization I of the EDX-course. The Matlab exercise was simple.
- Localization II covers sections 5.6.4-5.6.8. I covered chapter 5 until section 5.5 yesterday, so that nicely fits. Notice the correction on Slide 9 - eq. 2.
- Watched both the Markov and Kalman Filter lecture. The Problem set is using Matlab's anonymous functions.
March 3, 2025
- Looked what was covered in the last three lecturers covering chapter 4.
- The Milvius factury-AMR video is 6y old.
- Slide 11 showed the Nao sensor suite.
- Nice video on torque, to explain the working of a gyroscope.
- The optical gyroscope is nicely explained (American commercial style by iXblue.
- There is also a (Bosch) video of the working of an accelleration sensor.
- Nice Rviz visualisation of Ultrasonic sensor on a Turtlebot. The TS3 is no longer a product (had ROS Kinect support, 6cm wide with USB-B interface and Arduino connection), it is now a the Echo One. A bit larger (12.5 cm), and with a TPU to do the data-processing.
- Enthousiastic video of an (American East-coast) Tesla-user.
- Also showed an 11y old Visual SLAM video at before the break of the 2nd lecture.
- No videos for the last part of the lecture (Plane extraction with Laser Scanners).
- In the first part of the 3rd lecture an autonomous driving vehicle in Shenzhen is shown (2y old). Vehicle sees quite some edge-cases. Compared to the 2024 Tesla self-driving drive.
- BEV is shown with a NVIDIA end-to-end learning video (CVPR 2024).
- The Underwater VSLAM video no longer works.
- I like slide 117 with Bag-of-Words Pipeline, including a visual dictionary and histogram of patches.
- The KIVA video belongs to a IEEE Spectrum article from 2008 19y old.
- Slide 25 needs an update. Looking if this was also used in the Edx course.
- Looked at the Siegwart's first localization lecture. Goes directly into probabilistic localization. Stopeed for the moment at 3 minutes.
- Localization II is already Markov localization.
- The 2nd Localization I is a refresher on Probability Theory. Looks promissing, yet isn't. The 2nd Localization II comes the closest, with a description of Kalman Filter Localization (including the error-model F of the motion model).
- Looking at a good explanation how to get a ellips from a matrix. Looking into Cyrill's 5 minute videos. Looking first to his Localization video. Quite high-level, not going into details, just a list of what algorithms are possible (Kalman, Markov, etc), and that it is based on combining control and observations.
- So, didn't found what I was looking for. Best video was actually How to give a good lecture (more repetition!, reentry points!).
- So, better show this video, including the two eigenvalues and correlation coeficient
February 28, 2025
February 5, 2025
- Reading Chapter 7 (Robot Arm Kinematics) from Peter Corke's Robotics, Vision and Control.
- Used in WSL on nb-dual rvctool to see which robot-arms are part of the tool (models.list(type="URDF"). Continues further than the list on page 273, and contains for instance Willow Garage's PR2 and Nasa's Valkyrie, but no Nao robot.
- There are three types of definitions: "ETS", "URDF", "DH"). Would be nice to add the UMI-RTX and Mover5. A robot defined as "DH", can be converted to "ETS" format. A "URDF" model can also be converted to "ETS" format with method ets() (tested for models.URDF.Mico, which had no ETS-version).
- In section 7.4.1 the robot writes a letter 'B'. Would be nice to reproduce that with the UMI-RTX.
- In section 7.4.2 the gait of a simple 4-legged robot is worked out. Tried %run -m Walking, but that fails on method Cubiod() not known.
-
- Chapter 4 (Mobile Robot Vehicles) is also a good one to read.
- Interesting is the approach to drive a vehicle to a point (section 4.1.1.1) and to a line, before driving to a pose (section 4.1.1.4). The motion model used in the localization is introduced: converting the control to polar coordinates.
- Section 4.2 is about differential-steered vehicles. A picture of the Clearpath Robotics Husky is used as example.
February 4, 2025
- On slide 24 of the kinematics 2 link example I calculated the x, y position. It is in correspondence with the transformation elements of the SE(2) matrix on page 279, which is the forward kinematics of the 2-link example in Fig. 7.4b on page 257. Seems correct.
- There is a 3D-viewer version, but I didn't see how I could manipulate the joints q_i.
February 2, 2025
- Finished all lectures on Chapter 3, now time for the problem set.
- I like in Chapter 3.2 how the two constraint equations are slowly build up for the four wheel-types, I like from the EDX-lectures how they simplify the complex to simple equation of the fixed wheel. Maybe I should do both in my lecture: first build up slowly, thereafter break down again.
- I also like how the mobility comes from the rank of the constraint-matrix.
February 1, 2025
- The lecture on stacking the rolling constraints and the sliding constraints gives different forms of maneuverability. The comparison of the omni-drive example and the two-steer example is quite intuitive: same movement, but more time is needed to get the wheels into position. (slide 12 vs 13)
January 31, 2025
January 30, 2025
- Finished, Create Symbolic Matrices tutorial, continue with Create Symbolic Matrix Variables.
- Next is Use Symbolic Objects to Represent Mathematical Objects, which is using inverse trigonometric functions as example. Alos include systems of linear equations.
- Continue with Perform Symbolic Computations. Not only partial differentiation is possible, but also integration.
- Last tutorial is Use Assumptions on Symbolic Variables.
- I created rotation matrices with symmatrix([cos(alpha),sin(alpha),0;-sin(alpha),cos(alpha),0;0,0,1]) (x-axis) and symmatrix([cos(beta),0,sin(beta);0,1,0;-sin(beta),0,cos(beta)]), but this doesn't pass the test (no feedback).
- Tried a Devanit Hartenberg representation, but now I got the feedback that a 3x3 matrix is expected.
- Tried again, but now without symmatrix. Get feedback that R_B1 is wrong. Should try other direction (direction of angle).
- Now I see the error, rotated around z-axis, instead of the x-axis. Still R_B1 is wrong.
- Looked at this example. No ',' where used.
- That helped, I only expected another sign for gamma in R_23.
-
- Next assignment, I only have not seen the track to add another column to a matrix, so looking at video tutorial. Learned nothing new.
- Got a good hint from matrix in matlab.
- Looks all good, but I tried all 6 configurations, but r_3F_in3 stays wrong. Problem was that although I did subsitude, the class is still 'sym'. So, I first did tr_3F_in3 = [0 0 -l3]';, followed by r_3F_in3 = double(subs(tr_3F_in3,1)); (assume unit-lenght vectors).
- Next problems is that the Jacobian is defined with a function handle, trick was to convert to sym and also explcitly define the symbols for alpha, beta, gamma. Made a trivial implementation, by 8x code-repetition. The dr went down, until [0;0;0].
- The trajectory following makes a circle, but lags behind. Should use a PID, or watch the instruction-video again:
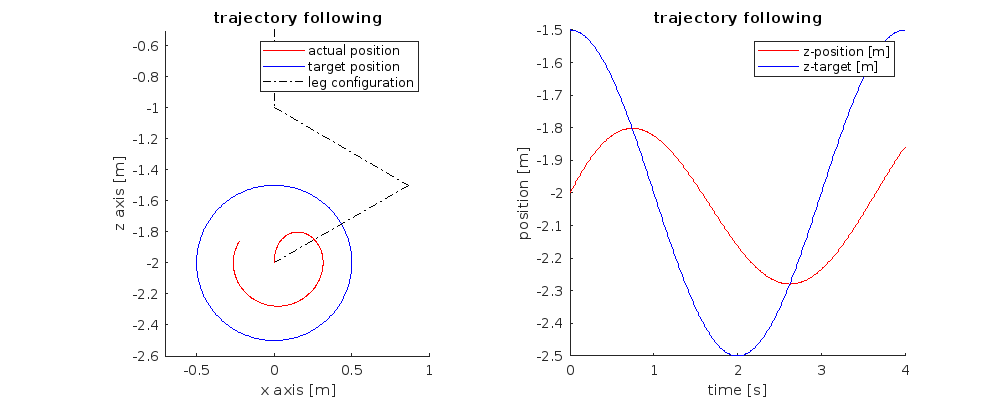
- Forgot to take the deltaT in acount (dr/dT), and to look at desired speed drGoal(t):
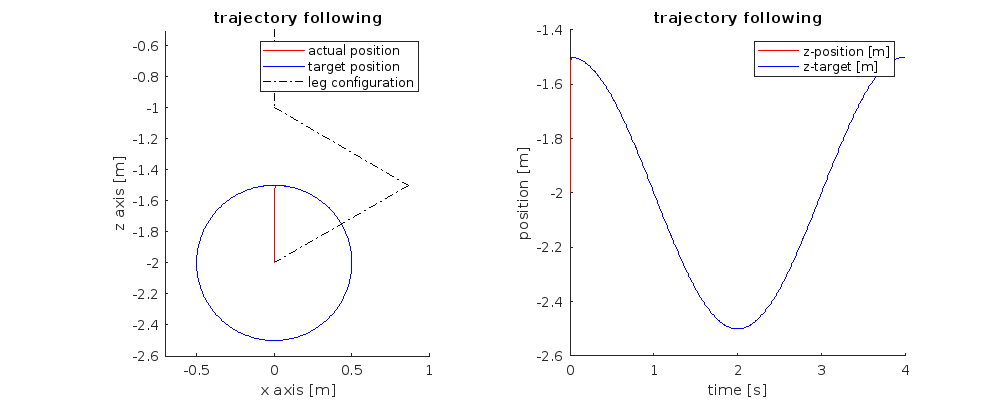
- Yet, this were all optional problems, so I finished 10% of the course but passing grade is still 0%. I finished Locomotion concepts, next section is Mobile Robot kinematics.
January 29, 2025
January 22, 2025
- On nb-dual I still have Matlab 2022a installed, although it have to be activated again.
- Activated it with my academic account.
- The symbolic toolbox was not installed, but I had that option. Could also upgrade to R2024b (not done yet).
January 17, 2025
- Explored the AMR at EDX already three times (2014, 2017, 2025).
- The 2017 progress was still 0%. 2014 is no longer working.
- Started with 2025 Introduction. They used three videos:
- So, all from the previous decade.
- Youtube gave me Inside the Lab: Taking Atlas From Sim to Scaffold (2024), which could replace the video Herke used.
- The introduction still used Lena (slide 7). The introduction focuses on three questions:
- Where am I?
- Where am I going?
- How do I get there?
- Followed by the see-think-act cycle. Each of the four components are shortly introduced.
-
- Next is Locomotion. Next to the textbook, also the following material is mentioned:
- Part A, Chapter 1 (Kinematics) of
B. Siciliano and O. Khatib, Springer handbook of robotics, Part A, Chapter 1 Kinematics. Berlin: Springer, 2008.
- Chapter 3 (Kinematics) and Chapter 4 (Rigid Multibody Systems) of
H. Bremer, Elastic Multibody Systems, Springer Netherlands, 2008.
- The How to Engineer a Dog would also be nice for Behavior-Baed Robotics.
- I like the final wrap up of the first segment of Introduction to Legged Robotics by Marco Hutter (slide 9) - 4% completed.
-
- I like the animations in slide 2 of Segment 2, which describes translation, rotation and screw motion.
- On slide 4 Tait-Bryan/Cardan angles (z-y-x) are defined (yaw, pitch and roll).
-
- The 3rd segment introduces generalize coordinates, which contains the un-actuated base and actuated joints in one vector.
- Marco goes fast, but I found his 2nd working example nice, where he gives an example of the Jacobian for a simple 3-Link arm.
- I like the animation of slide 4 showing the different solutions of inverse kinematics.
- No guidance on how to use the symbolic toolbox of Matlab before the first problem. (7% completed)
- The material in this course is not explictly govered in the book. Check Herke's lectures.
January 16, 2025
- Checked the presentations of last year.
- First lecture is course logistics and legs vs wheels.
- Looked at the Links
- The book's webpage still exists, but Slides links is broken (since Nov. 2015)
- The EDX version of course still exists. Could still enroll. Material is mostly video's, problem sets and Quizes. Last update seems 2020. The problem sets are in Matlab. First problem is to define three rotation matrices for a single leg. Tried just to fill in rotx(alpha), but they want the symbolic equation. Nice, but that would require to do Get Started with Symbolic Math toolbox.
- The Videos page still works, but contains videos from 2010.
- Also the Links page still works, didn't check them.
-
- The latest ETZH course is Spring 2021.
Previous Labbooks
Labbook2008.html
Labbook2007.html

