
![]()
![]()
![]()
![]()
Course Search, Navigate, and Actuate
"Zoeken, Sturen en Bewegen"
This is the information of year 2015.
The last two years the course was coordinated by Toto van Inge. His site could be found here.
In 2012 Arnoud Visser was also responsible for this course, the site
can be found here.
The experiments of the last week are listed on a separate page.
Description
The official description of course baiZSB6 can be found (in Dutch)
here.
Also a Blackboard portal to this information is available. Blackboard is mainly used for email and grading.
Contents
- Search Algorithms
Game playing is an example of type of problems that can easily decomposed in subproblems. For interesting games, like chess, the tree of subproblems grows to fast to be searched exhaustively, so other approaches are necessary. To solve the game we have to find a solution tree regardless of the opponent's replies.- MiniMax principle
- alpha-beta algorithm
- increasing the effectiveness with advice rules
- Path planning
You have had planning algorithms such as A* that work on graphs. So let's try to reformulate the path planning problem as a graph problem. These graphs are somewhat special, it is convenient to see them as discretized spaces because this leads to better implementations. So then we need the notion of configuration space to explain the graph's properties.- A* revisited
- Mapping path planning as graph search
- Task space and discretized configuration space
- Kinematics -> connectivity
- Criteria -> metric
- Obstacles -> forbidden nodes
- Examples: robot arm and self-parking car
- Other approaches of mapping path planning into graphs
- Trajectory planning
If you have setpoints, how to make it into a controllable path. - Rigid body motion
- physical rigid bodies as idealization
- physical space as vector space
- representing motions using linear algebra (coordinate-free)
- isometries
- proof of decomposition theorem: rigid body motion = rotation followed by translation
- coordinates: vector spaces in the computer
- rotation matrices: how to design them
- reference angles: Euler angles
- homogeneous coordinates
- Kinematics of linked mechanisms
- Denavit-Hartenberg notation
- Forward kinematics
- Inverse kinematics (briefly)
- Redundancy and degeneracy (briefly)
- Differential kinematics
Schedule
This schedule has some correspondance with the official schedule, but in case of doubt use the data on datanose.nl.
Download Lecturnity Player to listen to lecture, synchronized with the sheets.
| date | time | type | subject | location | lecturer/assistant | |
| Monday 1/6 | 15:00-17:00 | L0 | Course Overview Lecture pdf |
Turing zaal | Arnoud Visser | |
| Monday 1/6 | 15:00-17:00 | SCR1 | Searching through Game Trees - minimax and alpha-beta Lecture pdf |
Turing zaal | Arnoud Visser | minimax.pl, alphabeta.pl, follow_strategy.pl, advice.pl |
| Tuesday 2/6 | 13.00-15:00 | L1 | C1.110 | Path Planning Lecture, Recording | Leo Dorst | |
| Tuesday 2/6 | 9.00-17.00 | P1 | Task 1: Endgames | G0.23-25 | ||
| Wednesday 3/6 | 9.00-11:00 | L2 | Qualitative Navigation Lecture (pdf 1.1 Mb), recording (lpd 32 Mb) Distinctive Place Movie (88 Mb) Visual Homing Movie (15 Mb) |
Turing zaal | Arnoud Visser | Home-work article |
| Wednesday 3/6 | 9.00-17.00 | ZS | Task 1: Endgames | G0.23-25 | no assistance | |
| Thursday 4/6 | 11.00-17.00 | P2 | Task 1: Endgames | G0.23, G0.25 | ||
| Friday 5/6 | 9.00-11.00 | L3 | Quantative Navigation Lecture (pdf 194 Kb), recording lpd, Voronoi graph movies. |
C0.05 | Arnoud Visser | |
| Friday 5/6 | 9.00-17.00 | P3 | Task 1: Endgames | G0.23, G0.25 |
| date | time | type | subject | location | lecturer/assistant | |
| Tuesday 12/6 | 11.00-13.00 | L4 | Rigid body motionLecture, Recording | C0.110 | Leo Dorst | |
| Tuesday 12/6 | 13.00-19:00 | P4 | Task 2: Path planning module | G0.23, G0.25 | ||
| Tuesday 12/6 | 13.00-18.00 | PAV1 | Practicum Academische Vaardigheden | D1.160, A1.16B | no assistance | |
| Thursday 11/6 | L5 | Forward Kinematics Lecture, Recording | Leo Dorst | |||
| Wednesday 13/6 | 11.00-13:00 | P5 | Task 2: Path planning module | G0.12, G0.23, G0.25 | Toto van Inge | |
| Wednesday 13/6 | 13.00-17.00 | ZS | Task 2: Path planning module | G0.12, G0.23, G0.25 | no assistance | |
| Friday 12/6 | L6 | Inverse and Differential Kinematics Lecture, Recording | Leo Dorst | |||
| Thursday 13/6 | 11.00-13:00 | P6 | Task 2: Path planning module | G0.12, G0.23, G0.25 | ||
| Thursday 14/6 | 13.00-17.00 | ZS | Task 2: Path planning module | G0.12, G0.23, G0.25 | no assistance | |
| Friday 15/6 | 9.00-11.00 | No Lecture | ||||
| Friday 15/6 | 11.00-13:00 | P7 | Task 2: Path planning module | G0.12, G0.23, G0.25 | ||
| Friday 15/6 | 13.00-17.00 | ZS | Task 2: Path planning module | G0.12, G0.23, G0.25 | no assistance |
| date | time | type | subject | location | lecturer/assistant |
| Monday 13/6 | 9.00-17.00 | TO BE UPDATED | |||
| Tuesday 14/6 | 9.00-17.00 | P7 | Task 3: Inverse kinematics module | G0.23-G0.25 | |
| Wednesday 15/6 | 9.00-17.00 | P8 | Task 3: Inverse kinematics module | G0.23-G0.25 | |
| Wednesday 15/6 | 11.00-13.00 | Experiment0 | Brainstorming next week | G0.23-G0.25 | Arnoud Visser |
| Thursday 16/6 | 9.00-17.00 | P9 | Task 3: Inverse kinematics module | G0.23-G0.25 | |
| Friday 17/6 | 9.00-17.00 | Pres | demonstration and integration Task 2 and 3 | G0.23-G0.25 |
| date | time | type | subject | location | lecturer/assistant | |
| Monday 20/6 | 9.00-12.00 | Experiment1 | Kick-Off | G0.23-G0.25 | Arnoud Visser | |
| Monday 20/6 | 12.00-17.00 | ZS | G0.23-G0.25 | no assistance | ||
| Tuesday 21/6 | 9.00-17.00 | ZS | G0.23-G0.25 | no assistance | Wednesday 22/6 | 9.00-12.00 | Experiment2 | Mid-Term | G0.23-G0.25 | Arnoud Visser |
| Wednesday 23/6 | 12.00-17.00 | ZS | G0.23-G0.25 | no assistance | ||
| Thursday 23/6 | 9.00-17.00 | ZS | G0.23-G0.25 | no assistance | ||
| Friday 24/6 | 9:00-17.00 | Experiment3 | Demonstration and Documentation | G0.23-G0.25 | Arnoud Visser | |
| Friday 24/6 | from 17.00 | Experiment4 | Barbecue | near cantine | VIA |
It is not the result that counts, but your summery of your survey. Document your progress, experiments and decisions in a LabBook.
With a working system, and the acquired knowledge, you can explore new possibilities.
Here are the surveys of the previous years:
- the surveys of the 2011 students, see Experiment2010
- the surveys of the 2010 students, see Experiment2010
- the surveys of the 2009 students, see Experiment2009
- the surveys of the 2008 students, see Experiment2008
- the surveys of the 2007 students, see Experiment2007
- the surveys of the 2006 students, see Experiment2006
- the surveys of the 2005 students, see Experiment2005
- the surveys of the 2004 students, see Experiment2004
- Path-planning for a Hemisson-robot
- Talking mouth for a Aibo-robot
- Maze navigation with a Nao-robot
- Looking to a talking person with a Nao-robot.
- Extend the checkmate problem to more complex situations
- Refine the visualisation of the Virtual robot.
- Creating a gamepad interface for a virtual Aibo (Visual Basic)
- WiiBot RTX UMI
- Solve chess endgame with Monte Carlo tree search (MCTS)
- Hacking the Neato XV-11
- Programming the Concept Wheels of Ramon Lull.
You will be evaluated on your LabBook at the end of the week.
Evaluation
In 2012 the course was overall evaluated by the participants with a 7.7
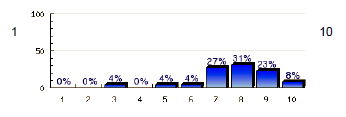 .
.
Literature

For the implementation in prolog we will look at chapter 24 of
Prolog Programming for Artificial Intelligence by
Ivan Bratko. The companion website of the 4th edition is not yet available, the companion website of the 3th edition contains several student resources.
This book was explored until chapter 13 in the previous course Logic Programming and Search Techniques.
Further we use the syllabus 'An Introduction to Robotics' by Leo Dorst, which is available for download at the Blackboard site.
Inheritance
In the old days, when Bachelors were not schooled at Dutch Universities,
a different course was given with another focus.
Still, much can be learned from the course 'Robotica'.
Last updated June 12, 2015
 This web-page ist of participants to this course is maintained by
Faculty
of Science
This web-page ist of participants to this course is maintained by
Faculty
of Science
University of Amsterdam
