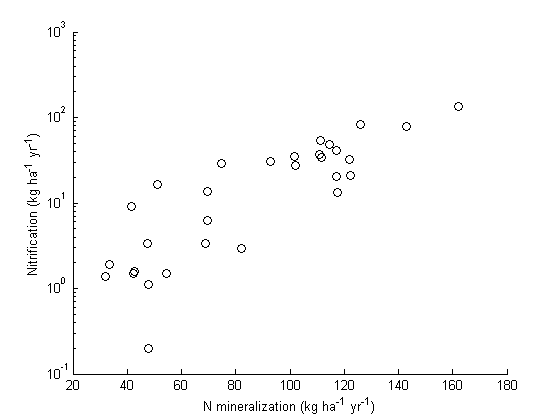
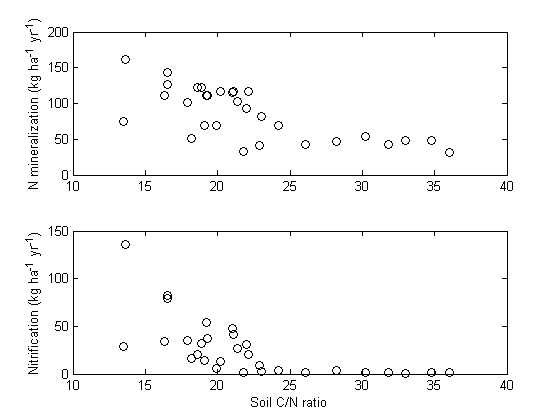
% regression_exercise.m % Ollinger et al. (2002) measured various plant and soil characteristics % (related to C and N processing) for 30 plots in the White Mountain National % Forest, New Hampshire, USA. Part of their analyses were aimed at estimating % the relationship between N mineralisation and soil C:N ratio and between % nitrification and soil C:N ratio. % % Here we draw scatterplots for these two relationships. % To see if there is any evidence for a nonlinear relationship. % % see: % Ollinger, S.V., Smith, M.L., Martin, M.E., Hallett, R.A., Goodale, C.L. & % Aber, J.D. (2002) Regional variation in foliar chemistry and N cycling % among forests of diverse history and composition. Ecology 83: 339-355. % Headerline in file olinger02.csv: % Plot,Species,History,FoliarN,Lignin,SoilCN,Nmineral,Nnitrif,FoliarLigN fid = fopen('ollinger02.csv'); data = textscan(fid, '%u%s%s%n%n%n%n%n%n','delimiter',',','Headerlines',1); fclose(fid); obsplot = data{1}; FoliarN = data{4}; Lignin = data{5}; SoilCN = data{6}; Nmineral = data{7}; Nnitrif = data{8}; FoliarLigN = data{9}; % to reproduce fig. 3 from study by Ollinger et al. 2002 % drawing the regression line is left as an exercise figure plot(Nmineral,Nnitrif,'ko') xlabel('N mineralization (kg ha^{-1} yr^{-1})') ylabel('Nitrification (kg ha^{-1} yr^{-1})') set(gca,'YScale','log') box off figure, subplot(2,1,1), plot(SoilCN,Nmineral,'ko'); ylabel('N mineralization (kg ha^{-1} yr^{-1})') subplot(2,1,2), plot(SoilCN,Nnitrif,'ko'); ylabel('Nitrification (kg ha^{-1} yr^{-1})') xlabel('Soil C/N ratio') % compare with fig. 4 in Ollinger et al. % Fit a linear model relation between N mineralisation and soil C:N % and nitrification to soil C:N ratio and examine the residuals. % Again, is a nonlinear relationship suggested? % Now fit a nonlinear, exponential, model of the form Y = ?*exp(?*X) % to each data set. What are the parameter estimates (cf. Ollinger et % al. p.343)? How much of the variation is explained by each model?