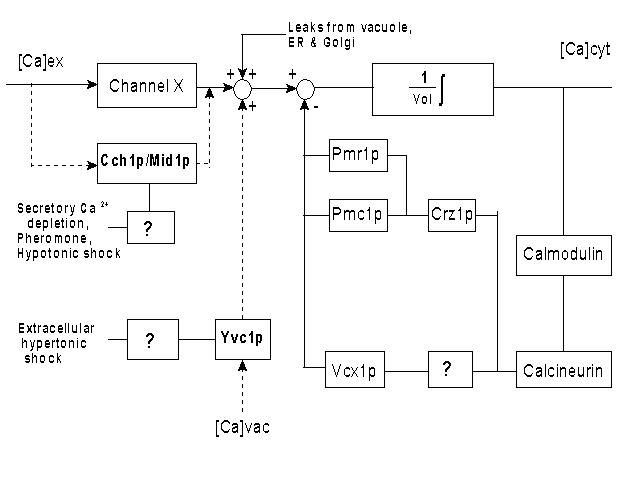
 Control Block Diagram used to model Ca homeostasis in yeast
Control Block Diagram used to model Ca homeostasis in yeast Mesoscale simulation paradigms for biological systems
 Control Block Diagram used to model Ca homeostasis in yeast Control Block Diagram used to model Ca homeostasis in yeast |
The project
The project is financed by the Netherlands Organisation for Scientific Research, NWO, research
program ``Wiskunde Toegepast'' and consists of 2 Ph.D. positions, one at the Section Computational
Science of the Universiteit van Amsterdam
(http://www.science.uva.nl/research/scs/)
and one at the Center for Mathematics and Computer Science in Amsterdam
(http://www.cwi.nl/htbin/pdels/frame?PDELB)
and several other researchers from the UvA, VU and CWI (see
below: ``The research team''). This project is carried out within the framework of the Silicon Cell
Initiative Amsterdam (http://www.siliconcell.net/sica/)
Abstract
A major challenge in the computer simulation of biological systems is the
treatment of the vast temporal and spatial scales.
Nowadays, one can observe biological systems in great detail, but often at the
cost of other important attributes of the system. Without ``disturbing'' the
system it is possible to see - with the naked eye - structures of up to 200
$\mu$m such as a large cell. With a light microscope one can distinguish
the compartments of a human cell, and with an electron microscope one can even see
very small details such as proteins, but observations on the reactions between
proteins are beyond current experimental capabilities. Computer simulations
have comparable resolution regimes. In the microscopic approach (molecular dynamics or
Monte Carlo methods) one examines systems at the level of atoms or proteins.
At present one can examine systems up to the order of 10^5 atoms on time
scales up to nanoseconds with these detailed simulations. This is still orders
of magnitude below the scales needed to model, for example, a living cell.
In the macroscopic regime, continuum-based simulations (using systems of
partial differential equations) model complete
biological assemblies but do not contain any explicit molecular information.
For example, most current models of the metabolism in a cell are either based on
a qualitative steady-state analysis or on the assumption that the cell is
homogeneous in the concentration of the different proteins.
In the proposed project we want to develop and compare computational models of parts
of the living cell that can calculate in detail system properties from
experimentally obtained molecular and physical-chemical data.
Such a model is as close as
possible to the biological experiments and therefore can be used not only for
understanding the principles of function but also to steer further biological
experiments. We focus on two subjects: (i) simulation of reaction-diffusion phenomena with
non-trivial chain-like reaction mechanisms in three dimensions, and
(ii) incorporating real data, as obtained from confocal microscopy, into the model.
The latter includes coupling of the reaction-diffusion model at fractal-like interfaces
with a model (for example an aggregation model) of a dynamically changing interface.
We want to compare two different model approaches in the mesoscopic
regime: the first using particle-based methods (lattice Boltzmann) and the
second using methods based on partial differential equations (PDEs). We
will compare the simulated results from both methods with each other
and with actual observations on both types of reaction mechanisms.
The research topic at the Section Computational Science is the development of particle-based
methods (e.g. Lattice Boltzmann) for reaction-diffusion systems with irregular, dynamically
changing, interfaces. As a first test case this approach will be used to model the Ca homeostasis
in yeast. The aim of the combined project is to compare this particle-based method
with a continuum approach (developed by the second Ph.D. student at the Center for Mathematics)
for problems with large spatial and temporal scales such as arise, e.g., in the study
of biological cells.
The Research Team
Section Computational Science (UvA)