From the entry "Linkages" in the Encyclopedia Brittanica, 1958.
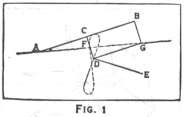
It was essentially a three bar motion, ACDE (fig.1), the links of which were so adjusted in length and disposition as to cause a point F on the traversing link CD to describe a figure of 8. The portion of the curve near the point of inflection is nearly straight for an appreciable length. If the two links AC and DE which rotate about the fixed points A and E are of equal length and the point F is in the middle of CD, the figure of 8 is symmetrical; but if they are of unequal lengths, one limb of the curve is straighter than the other and is straightest when the point F is taken so that CF:FD as DE:AC. If the head of the piston rod were fixed at F it is clear that the point E would be an an inconvenient distance from the rest of the engine; so Watt added two more links, BG and DG, forming a parallellogram, and it will be seen that ACDGB forms a pantograph in which the usual tracing point and fixed centre have changed places; and now if AC:CB as CF:FD, the point G will describe a curve similar to that described by F. The head of the piston rod was attached to G.
Several attempts were made in the early part of the 19th century to improve upon Watt's parallel motion (...) But it was reserved to Peaucellier, a lieutenant in the French army, to invent the first exact parallel motion. In 1864 he produced his famous Peaucellier cell, consisting of six links, which converts rotary motion into a truly straight line. It seems, however, to have completely escaped notice. Prof. Chebyshev of the University of St. Petersburg had been very interested in parallel motion without having arrived at any solution. But a pupil of his, named Lipkin, rediscovered the Peaucellier cell. The invention was introduced in England where it caused great admiration and interest, forming the subject of an address by Prof. Sylvester at the Royal Institution in 1874.
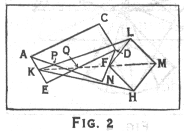
It consists of four equal bars, FL, LM, MH, HF, and two other longer equal bars KH and KL, jointed together as shown in fig.2. The outstanding property of this simple mechanism is that during its deformation KF.KM remains constant; so that if K is fixed, the curves traced out by F and M are inverse curves. If F describes a circle, M will describe the inverse circle; but if the centre of the F circle is at a distance from K equal to its radius, then the radius of the M circle becomes infinite; i.e. M describes a straight line.
This form of parallel motion is stated to have been used in an engine installed for the purpose of ventilating the Houses of Parliament before the introduction of electric fans.
For a LEGO model of the Peaucellier cell, click here, for a JAVA applet here.

After Sylvester's lecture, a period arose in England during which much attention was paid to the subject of linkages, notable by Sir A.B. Kempe and H. Hart. Chebyshev had proved to his own satisfaction that no linkage of five bars could accurately convert circular motion into rectilinear motion; but in 1877 Hart produced one (Proc. Lond. Math. Soc.), thus showing the danger of trying to prove a negative. He had also previously invented one of four links (Messenger of Mathematics, 1875).
This mechanism consisted of a crossed
parallellogram EAND (fig. 2), formed by rotating the
triangle ACD about the diagonal AD. If any straight line KF be drawn
parallel to AD or EN, cutting the links AN and ED in P and Q, then KP.KQ is
a constant; so that if K is fixed, the point P and Q describe inverse curves.
If the link AE is fixed and K is in the midpoint of AE, F will descibe the inverse of a conic; and if we add a Peaucellier cell KLMHF, M will describe the
conic. If ED:EA as 1:sqrt(2), F describes a lemniscate and M a rectangular
hyperbola.