|
double zeroPoint(pf, pzf, double, double, double);
// return zeropoint of function f using method m
in interval [lbnd..ubnd] with precision eps
double zeroPoint(pf f, pzf m,
double lbnd, double ubnd, double eps) {
return(m(f, lbnd, ubnd, eps)); // actual code!!
}
int main(void) {
printf("zeroPoint of test using secant: %20.18f\n",
zeroPoint(testFunction, secantMethod, 0.0, 1.0, 1E-10));
}
There is a lot more to say about higher-order functions:
• The concept is powerfull and leads to clear, clean and concise code.
• Read any textbook on functional programming (language Haskell).
• Java did not inherit the concept of formal function parameters from C.
• In Java anonymous inner classes are designed for this purpose.
• In the discussion of lists and trees we will introduce and apply
higher-order functions again (processList and processTree).
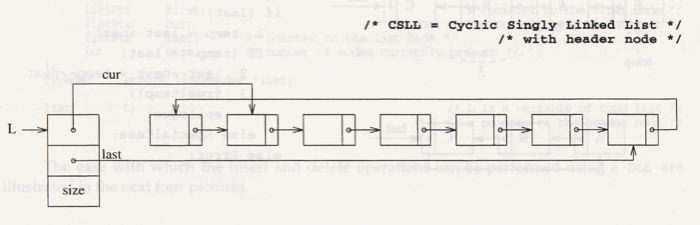
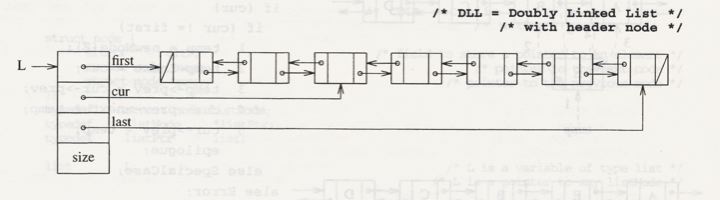
|
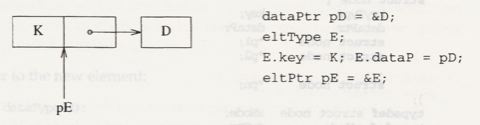
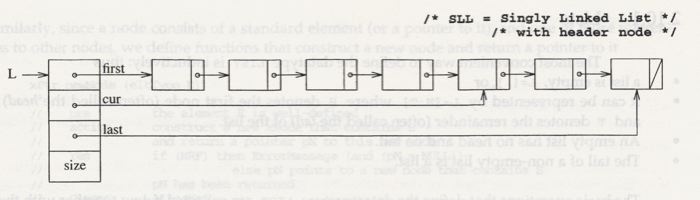
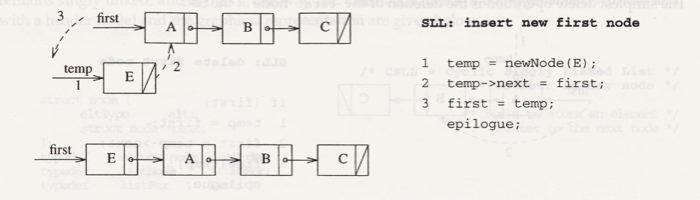
API

|










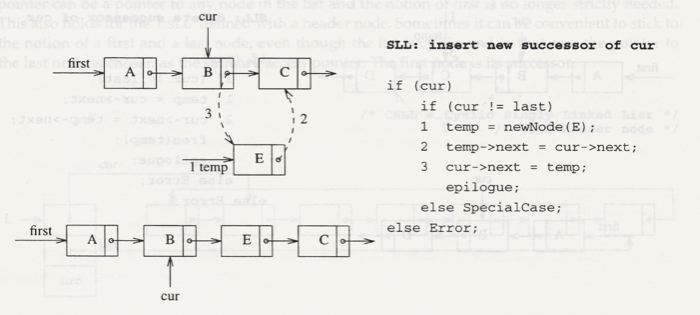
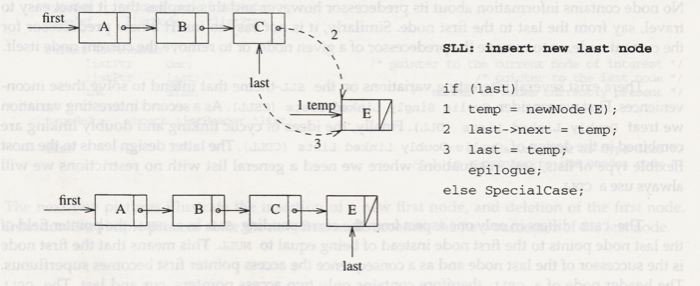
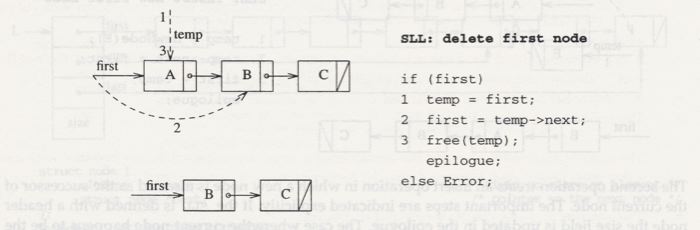 and in the next
and in the next 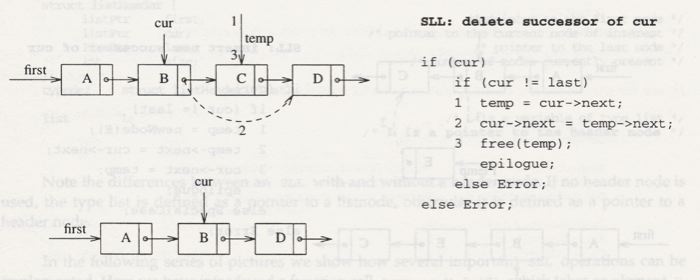
 •
•