Design decisions

22.01

The concept of list interface:
applying datastructure hiding and encapsulation.
A list interface is a collection of functions (prototypes) that act on lists 
including the documentation for the programmer.

Design decisions for elements:
•	an element is a struct that contains a positive integer key 
	and a pointer to data.

Design decisions for methods:
•	Any function that changes the list 
	•	by changing the structure of the list, or
	•	by changing the contents of the list
	imports the original list and returns the modified list.
•	A function that only inspects the list returns void.
•	Functions that perform a check on the list return a boolean.
etc.

NEVER EVER 
LET YOUR FUNCTION PERFORM A MORE COMPLEX TASK 
THAN ITS NAME SUGGESTS!!                               BUT ...	

22.01

TABLE OF CONTENTS HC 22

22.02

List interface (1)

22.02

 
list createList();
/*
//	pre    true
//	action create a new empty list and return the new list
//	res    a new empty list exists
//	usage  list L = createList();
*/
list destroyList(list L);
/*
//	pre    list L exists
//	action returns a new empty list
//	res    a new empty list 
//	usage  list L = destroyList();
*/

bool isEmptyList(list L);
/*
//	pre    list L exists
//	action determine whether list L is empty or not
//	res    true if the list is empty and false otherwise
//	usage  if (isEmptyList(L)) {...}
*/

22.01

TABLE OF CONTENTS HC 22

22.03

List interface (2)

22.03

bool isFullList(list L);
/*
//	pre    list L exists
//	action determine whether list L is full or not
//	res    true if the list is full and false otherwise
//	usage  if (isFullList(L)) {...}
*/

list insertFirst(eltPtr pe, list L);
/*
//	pre    list L exists and pe refers to an element e
//	action insert element e as the new first element of list L
//	res    a new list with first element e 
*/
list insertLast(eltPtr pe, list L);
/*
//	pre    list L exists and pe refers to an element e
//	action insert element e as the new last element of list L
//	res    a new list with last element e
*/

22.02

TABLE OF CONTENTS HC 22

22.04

List interface (3)

22.04

 
list deleteFirst(list L);
/*
//	pre    list L exists and is not empty
//	action delete the first element of list L
//	res    the first element has been removed
*/
list deleteLast(list L);
/*
//	pre    list L exists and is not empty
//	action delete the last element of list L
//	res    the last element has been removed
*/

dataPtr getData(keyType k, list L);
/*
//	pre    list L exists and is not empty
//	action return the data of the element with key k
//	       if no such element exists then return NULL
//	res    pointer to the data characterized by key k
//	       if no such key exists then NULL
*/

22.03

TABLE OF CONTENTS HC 22

22.05

List interface (4)

22.05

list setData(keyType k, dataPtr pd, list L);
/*
//	pre    list L exists and is not empty
//	action replace the data of the element with key k 
//         by data d pointed at by pd
//	       if no element with key k exists then no action
//	res    list L after updating element with key k
*/

int sizeOfList(list L);
/*
//	pre    list L exists
//	action determine the number of elements of list L
//	res    the number of elements
*/
list copyList(list L);
/*
//	pre    list L exists
//	action construct a copy of list L and return the copy
//	res    the original list still exists!!
//	       and the copy is returned by the function
*/

22.04

TABLE OF CONTENTS HC 22

22.06

List interface (5)

22.06

list sortList(list L);
/*
//	pre    list L exists
//	action rearrange the elements according to keyvalue
//	       and return the sorted list
//	res    the sorted list is returned by the function
*/

void traverseList(list L);
/*
//	pre    list L exists and is not empty
//	action visit all nodes from first to last (and print keys)
//	res    true
*/
list processList(list L, eltPtr f(eltPtr));
/*
//	pre    list L exists and is not empty
//	action visit all nodes from first to last 
//	       and process elements by application of function f
//	res    the processed list
*/

22.05

TABLE OF CONTENTS HC 22

22.07

Design decisions for list structure

22.07

The last function ProcessList is a higher-order function. 
All elements of the list are processed by the user-defined function f. 
This function imports a pointer to element and 
returns a processed version of the element: eltPtr f(eltPtr);

Now what remains is the actual choice for the list structure 
	array?, sll?, csll?, dll?, cdll?, ...
and the implementation of the functions that are listed in the above interface.

Design decisions for the datastructure:
•	a listnode is a struct that contains a pointer to an element 
	and pointers to the previous and to the next node
•	a listpointer is a pointer to a listnode
•	a listheader is a struct that contains pointers to first and last node
	and it contains a member that holds the number of nodes
•	a list is a pointer to a listheader.

In C the interface is written in the headerfile list.h. 
the implementation is written in the sourcefile list.c.

22.06

TABLE OF CONTENTS HC 22

22.08

Stack: last in first out!

22.08

The stack is a time-ordered list with a very restricted set of operations. 
The time-order of the elements on the stack is fixed by their time of arrival 
and the only element that can be accessed is the element that arrived most 
recently. This element is called the top of the stack.

Insert and delete are therefore equal to the list functions insertFirst 
and deleteFirst and the operations are called Push and Pop.
 
The basic operations that define the datastructure stack:

•	The function create creates a new and empty stack: 
	create() = [ ]
•	The function push adds a new top (with element E) to the stack: 
	push(E, S) = [E:S]
•	The function pop removes the top from the stack: 
	pop(S) = T iff S = [E:T]
•	The function top inspects the top of the stack: 
	top(S) = E iff S = [E:T]

22.07

TABLE OF CONTENTS HC 22

22.09

Stack axioms

22.09

Hence the axioms for the basic operations can be stated as:

•	isEmpty(create())   = TRUE
•	isEmpty(push(E, S)) = FALSE

•	top(create())       = ERROR (error in Top: Empty Stack)
•	pop(create())       = ERROR (error in Pop: Empty Stack)

•	top(push(E, S))     = E
•	pop(push(E, S))     = S

Auxiliary functions
•	the partner of isEmpty is called isFull
•	the partner of create is called destroy
•	the partner of top is called bottom
•	traverse from top to bottom and from bottom to top
•	...

22.08

TABLE OF CONTENTS HC 22

22.10

Stack interface

22.10

These considerations then yield the following C-interface for stack:

stack createStack();             // create a new empty stack

bool isEmptyStack(stack s);      // check empty or not
bool isFullStack (stack s);      // check full or not
int  sizeOfStack (stack s);

stack push(stackElt e, stack s); // add e on top if not full
stack pop(stack s);              // remove top if not empty
stackElt top(stack s);           // get top if not empty

void showStack(stack s);

This interface must be implemented in  PR21 

22.09

TABLE OF CONTENTS HC 22

22.11

Stack structure

22.11

   

	struct node {
	   eltPtr eltP;        // store pointer to an element
	   struct node *link;  // link to previous node on stack 
	};
	typedef struct node stackNode;
	typedef stackNode*  stackPtr;

	struct header {
	   stackPtr top;       // pointer to the top of the stack
	   int      size;      // number of nodes currently present
	};
	typedef struct header stackHeader;
	typedef stackHeader* stack;

The stack operations are exactly the same as in PR 1 
The interface should  not change!
 PR22 

22.10

TABLE OF CONTENTS HC 22

22.12

Implementation of stack (SLL)

22.12

 The implementation of the stack from PR21 

 The implementation of the stack (SLL) from PR22 

22.11

TABLE OF CONTENTS HC 22

22.13

Queue: first in first out!

22.13

The queue is a time-ordered list with a very restricted set of operations. 
The time-order of the elements on the queue is fixed by their time of arrival.
Elements arrive at the rear end of the queue and are served at the front.
Thus the element that arrived first is also the element to be served first and
the element that arrived last will be the last one to be served.
Insert and delete are therefore equal to the list functions insertLast 
and deleteFirst and the operations are called enqueue (add or insert) and 
dequeue (serve, delete or remove).
The basic operations and axioms that define the datastructure queue: 

•	The function create creates a new and empty queue: 
		create() = [ ]
•	The function enqueue adds a new node at the rear end: 
		enqueue(E,Q) = [Q:E]
•	The function dequeue  removes the node at the front: 
		dequeue(Q) = T iff Q = [E:T]
•	The function front inspects the front end of a queue: 
		front(Q) = E iff Q = [E:T]
•	The function rear inspects the rear end of a queue: 
		rear(Q) = E if and only if Q = [T:E]

22.12

TABLE OF CONTENTS HC 22

22.14

Queue axioms

22.14

Hence the axioms for the basic operations are:

•	isEmpty(create())     = True
•	isEmpty(enqueue(E,S)  = False

•	front(create())       = error in front: Empty Queue
•	front(enqueue(E,Q))   = if isEmpty(Q) 
	                        then E 
	                        else front(Q)
•	rear(create())        = error in rear: Empty Queue
•	rear(enqueue(E,Q))    = E

•	dequeue(create())     = error in dequeue: Empty Queue
•	dequeue(enqueue(E,Q)) = if isEmpty(Q) 
	                        then create() 
                             else enqueue(E, dequeue(Q))

22.13

TABLE OF CONTENTS HC 22

22.15

Queue interface

22.15

The C-interface for queue:

queue createQueue();             // create a new empty queue

bool isEmptyQueue(queue q);      // check empty or not
bool isFullQueue (queue q);      // check full or not

queue insert(queueElt e, queue q);  // add e to rear if not full
queue serve(queue q);               // serve front if not empty
queueElt front(queue q);            // get front if not empty
queueElt rear(queue q);             // get rear if not empty

This interface must be implemented in  PR21 
where a queue is designed using two stacks (of the type discussed above).
Notes: 
	stack in is used to enqueue elements
	stack out is used to serve elements
	if out is empty and serve is called 
	then
	   transfer the elements from in to out 
	   and perform the serve operation on the top of out

22.14

TABLE OF CONTENTS HC 22

22.16

Queue structure

22.16

Queue implemented as an SLL or CSLL with header.
First the declaration (SLL):

	struct node {
	   eltPtr eltP;
	   struct node *link;
	};
	typedef struct node queueNode;
	typedef queueNode*  queuePtr;

	struct queueHeader {
	   queuePtr front; // pointer to the front of the queue
	   queuePtr rear;  // pointer to the rear of the queue
	   int      size;  // number of nodes currently present
	};
	typedef	struct queueHeader* queue;

	queue Q;          // Q is a variable of type queue
	                  // Q is a pointer to the header node

 On the next slide the graphical representation (CSLL)

22.15

TABLE OF CONTENTS HC 22

22.17

Queue (CSLL)

22.17

As a variation on this theme you will implement the CSLL design 
where only the pointer rear is supported!  PR22  
This design leads to an efficient implementation for all queue operations.



	struct node {
	   eltPtr eltP;
	   struct node *link;
	};
	typedef struct node queueNode;
	typedef queueNode*  queuePtr;

	struct queueHeader {
	   queuePtr rear;     // pointer to the rear of the queue
	   int      size;     // number of nodes currently present
	};
	typedef struct queueHeader* queue;

22.16

TABLE OF CONTENTS HC 22

22.18

Implementation of queue (CSLL)

22.18

 The implementation of the queue from PR21 

 The implementation of the queue (CSLL) from PR22 

22.17

TABLE OF CONTENTS HC 22

22.19

BUT ...

22.19

Design decisions for methods. 
Alternative points of view exist!!
Any function that changes the list 
•	by changing the structure of the list, or
•	by changing the contents of the list
	imports the original list and exports the modified list
	using a formal reference parameter,
	and returns a boolean the value of which indicates 
	whether or not its action was successful (2),
	and even this boolean can be exported by reference 
	in which case the function returns void (3). 

Example:
•	list deleteFirst(list L);    // previous design decision
•	bool deleteFirst(list* L);    // 2
•	void deleteFirst(list* L, bool* deleted); // 3

 Back to 22.01

Design decisions can have a severe impact on implementation details!! 
Next 4 sheets!!

22.18

TABLE OF CONTENTS HC 22

22.20

InsertLast in bare SLL

22.20

Consider the simplest SLL declaration you can imagine:

	typedef int eltType;  // elements are integer
	typedef struct listNode* listNodePtr;
	typedef struct listNode {
	   eltType elt;
	   listNodePtr next;
	} listNode;
	typedef listNodePtr list;  // renaming listNodePtr to list

The first question of interest is how to declare a method that
inserts a new element as the last element of an existing list? 

•	declare a function that imports an element E and a list L
	and returns the new list [L:E] as its return value
	
	list insertFunc(eltType E, list L);

•	declare a procedure that imports an element E and a list L
	and exports the new list [L:E] using a reference parameter
	
	void insertProc(eltType E, list* L);

22.19

TABLE OF CONTENTS HC 22

22.21

Recursion vs iteration

22.21

In the sequel we will not use a boolean to report success or failure!

The second question of interest is how to define a method that
inserts a new element as the last element of an existing list? 
Well, since the problem does not support a pointer to the last node
the last node must be found and then its next field should point to a
new node that contains element E. 
If pointer p refers to the last node then p->next is equal to NULL
and must be replaced by a pointer to the new node with element E.

•	recursive implementation: the function calls itself in order to
	find the last node
	see insertFuncRec and insertProcRec

•	iterative implementation: a for- or while-loop is used to find 
	the last node
	Two techniques are of interest (1) and (2)
	see insertFuncIter and insertProcIter
	

22.20

TABLE OF CONTENTS HC 22

22.22

Function vs procedures

22.22

	list insertFuncRec(eltType E, list L) {
	  if (!L)
	    L = newList(E, NULL);
	  else
	    L->next = insertFuncRec(E, L->next); // recursion
	  return(L);
	}


	void insertProcRec(eltType E, list *L) {
	  if (!*L)	
	    *L = newList(E, NULL);
	  else	
	    insertProcRec(E, &(*L)->next);       // recursion
	}

where we used the auxiliary function newList that imports element E
and returns a pointer to a listnode with next equal to NULL.

22.21

TABLE OF CONTENTS HC 22

22.23

Implementation details (1)

22.23

	list insertFuncIter1(eltType E, list L) {
	  if (!L)	
	    L = newList(E, NULL);
	  else {
	    listNodePtr p = L; // p is ptr to listNode
	    while (p->next) 
	      p = p->next; // loop exit: p refers to the last node
	    p->next = newList(E, NULL); // set p->next
	  }
	  return(L);	
	}
 
	list insertFuncIter2(eltType E, list L) {
	  listNodePtr *p = &L;// p is ptr to ptr to listNode!!
	  while (*p) 
	    p = &(*p)->next; // loop exit: p is equal to the 
	                     // address of next of last node
	                     // value of p ie *p is equal to NULL
	  *p = newList(E, NULL); // and now p gets its proper value 
	  return(L);	
	}

22.22

TABLE OF CONTENTS HC 22

22.24

Implementation details (2)

22.24

 

	void insertProcIter1(eltType E, list *L) {
	  if (!*L)	
	    *L = newList(E, NULL);
	  else {
	    listNodePtr p = *L;// p is ptr to listNode
	    while (p->next)
	      p = p->next;
	    p->next = newList(E, NULL);
	  }
	}

	void insertProcIter2(eltType E, list *L) {
	  listNodePtr *p = L;// p is ptr to ptr to listNode
	  while (*p) 
	    p = &(*p)->next; 
	  *p = newList(E, NULL);
	}

Be sure to understand the essential differences 
between the iterative implementations type 1 and 2. NOTES...

22.23

TABLE OF CONTENTS HC 22

22.25

Trees

22.25

Quite another part of the toolkit deals with hierarchical structures  
known as trees. The simplest tree is a Binary Tree (BT).
A binary treenode has the same structure as a doubly linked list node.
 
Both nodes contain a field where an element and two pointers can be stored. 
In a DLL node these pointers point to predecessor and successor nodes. 
This gives the datatype its linear structure. 

The pointers in a BT node are said to point to the descendants (or children) 
of the node under consideration (the parent). 
This gives the datatype its hierarchical structure. 

We will discuss three types of tree:

•	Binary Tree (BT): each node is allowed to have at most two children.
 
•	Binary Search Tree (BST): This type of tree is again a BT but now the 
	nodes are ordered using their key values. 

•	General Tree: Here each parent can have as many children as (s)he likes. 

22.24

TABLE OF CONTENTS HC 22

22.26

Binary trees

22.26

 
A binary tree is most conveniently defined in an inductive way
	a binary tree is empty,
		T=[ ]
	or it is not empty and can be represented by
		T = [lhs:root:rhs] 

Here 
	root denotes the very first node of the tree, 
	lhs stands for the subtree on the left and
	rhs for the subtree on the righthand side. 
	An empty binary tree has no root and no subtrees.

The subtrees of a non-empty binary tree are binary trees (that can be empty).

INTERMEZZO: Inductive definitions lead to natural recursive implementations!
Example: determine the size of a binary tree (the number of nodes in the tree).

22.25

TABLE OF CONTENTS HC 22

22.27

Constructors and accessors

22.27

 
Indeed,
•	an empty binary tree has no nodes (size 0)
•	otherwise the tree consists of a root node and two subtrees (lhs and rhs)
	and its size equals 1 plus the sizes of its two subtrees.
Thus:
	theSizeOf(tree t) =
	  isEmpty(t)   => 0
	  otherwise    => 1 + theSizeOf(lhs) + theSizeOf(rhs)

The basic operations that define the datastructure BT 
are collected below together with the axioms that must be satisfied. 

First we define the functions create and construct,
and three access functions called root, lhsChild and rhsChild. 
 
The function create creates a new and empty binary tree: 
	create() = [ ].
The function construct takes two binary trees, say L and R, and an element E,
and constructs a new binary tree where E becomes the element of the root and
L and R the subtrees on the left and right, respectively: 
	construct(L,E,R) = [L:E:R ].

22.26

TABLE OF CONTENTS HC 22

22.28

Axioms

22.28

 
In order to access the elements of a binary tree we need functions that 
retrieve the element at the root and that give access to 
the rootnodes of the left- and right subtree (root, lhsChild and rhsChild). 

The axioms for the basic operations can now be stated as:

	isEmpty(create())          = true
	isEmpty(construct(L, E, R) = false

	lhsChild(create())           = Error(Empty Tree)
	root(create())               = Error(Empty Tree)
	rhsChild(create())           = Error(Empty Tree)

	lhsChild(construct(L, E, R)) = L
	root(Construct(L, E, R)      = E
	rhsChild(construct(L, E, R)) = R

22.27

TABLE OF CONTENTS HC 22

22.29

More operations

22.29

These axioms might be extended by delete operations. 
For the moment we introduce a delete operation that removes the left or right 
subtree of the root as a whole

	removeL(create())           = Error(Empty Tree.)
	removeR(create())           = Error(Empty Tree.)
	removeL(construct(L, E, R)) = [[]:E:R]
	removeR(construct(L, E, R)) = [L:E:[]]


Declaration and graphical representation.

The following declaration defines a binary tree with a header node that gives 
access to the root of a binary tree. In the picture we have decorated the header 
node with additional pointer fields, such as pointers to the leftmost and to
the rightmost node of the tree.

22.28

TABLE OF CONTENTS HC 22

22.30

Declaration of BT

22.30

 


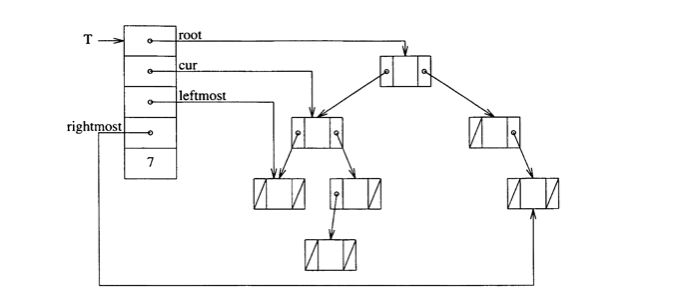Key, dataType, dataPtr, eltType and eltPtr are as usual. 

	typedef struct treeHeader {
		treePtr root, cur;
		treePtr lmost, rmost;
		int     size;
	} treeHeader;
	typedef treeHeader* tree
	tree myTree, yourTree, ourTree, T;

22.29

TABLE OF CONTENTS HC 22

22.31

Announcement

22.31

Here we do not continue the discussion on general binary trees 
but we will restrict our interest to 
BINARY SEARCH TREES (BST).

NB: In the sequel we do not use header nodes!

22.30

TABLE OF CONTENTS HC 22

22.32

Notes

22.32

How do you change the value of a variable?
•	by direct assignment:  var = val;
•	by indirect assignment:  ptr2var = &var; *ptr2var = val;

Now consider adding a new last node with content e to an existing list:
•	if pointer last to the last node is supported then
		last->next = createNode(e);
•	if pointer last to the last node is not supported then
		listPtr p = first;
		while (p->next) p = p->next;
//	now p satisfies p->next == NULL and gets its new value by direct
//	assignment  p->next = createNode(e);
•	It should be clear that 
		listPtr p = first;
		while (p) p = p->next; p = createNode(e);
	does not link a new last node to the list.
•	And 
		listPtr* p = &first;
		while (*p) p = &(*p)->next; *p = createNode(e);
	is what you need!
 Back to 22.24

22.31

TABLE OF CONTENTS HC 22

22.01

TABLE OF CONTENT HC 22

TOC

TOC