Abstracts
|
Jean Mémin: On the robustness of backward stochastic differential
equations
In this talk we study the robustness of backward
stochastic differential equations (BSDE in short) with
respect to the Brownian motion; more precisely we will show that if
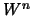 is a martingale approximation of a Brownian motion is a martingale approximation of a Brownian motion 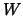 then the solution of the BSDE driven by the martingale
then the solution of the BSDE driven by the martingale 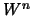 converges to the solution of the classical BSDE, namely the
BSDE driven by
converges to the solution of the classical BSDE, namely the
BSDE driven by 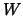 . Here we will not assume that . Here we will not assume that 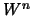 has
the predictable representation property. As a byproduct of the result
we obtain the convergence of the "Euler scheme" for BSDEs
corresponding to the case where has
the predictable representation property. As a byproduct of the result
we obtain the convergence of the "Euler scheme" for BSDEs
corresponding to the case where 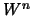 is a time discretization of is a time discretization of 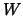 . .
|
Harry van Zanten: On Donsker Theorems for Additive Functionals of Ergodic Diffusion
Processes
In this talk we discuss
the uniform central limit problem for additive
functionals of an ergodic, 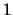 -dimensional diffusion process.
We consider a regular diffusion -dimensional diffusion process.
We consider a regular diffusion 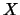 on an open interval on an open interval 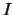 , with finite
speed measure , with finite
speed measure 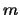 and diffusion local time and diffusion local time
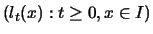 .
If .
If 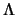 is a collection of signed measure on is a collection of signed measure on 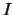 and the
total variations of these signed measures are uniformly bounded,
we give a sufficient condition on and the
total variations of these signed measures are uniformly bounded,
we give a sufficient condition on 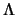 under which the random map under which the random map
converges weakly, as 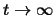 , to a tight weak limit in the space , to a tight weak limit in the space
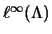 of bounded functions on
of bounded functions on 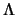 . The condition on . The condition on 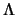 is formulated
in terms of the metric entropy of the class with respect to a suitable metric.
We also discuss a number of applications of the abstract result. is formulated
in terms of the metric entropy of the class with respect to a suitable metric.
We also discuss a number of applications of the abstract result. |
Marc Yor: On subordinators, self-similar Markov processes and some factorizations of the
exponential variable
In this lecture, I shall prove that if
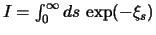 is the
`exponential functional' associated to is the
`exponential functional' associated to
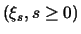 , a subordinator, then it
is always a factor in a multiplicative decomposition of the exponential variable.
I shall illustrate this result with several examples. , a subordinator, then it
is always a factor in a multiplicative decomposition of the exponential variable.
I shall illustrate this result with several examples.
|