Information synergy
Synergy is important but often neglected by scientists because it is unknown how to quantify it. We propose a new path in the ongoing quest.
Synergy occurs when a collection of units is correlated with another system whereas none of the individual units are correlated. This phenomenon plays a crucial role in the vast majority of dynamical systems studied by science, including in biology, finance, and social networks — without at least some degree of synergy they can simply not function. However it is often neglected by scientists. The primary reason for this surprising fact is that it is currently unknown how to mathematically define synergy, let alone calculate it from data or study it from experiments.
Informally speaking, synergy is the act of integrating information from different sources into something new. Think of your current opinion about, say, eating meat. It is the result of your past personal experiences, what you have seen in the media, and the opinions of your friends and family members. Yet your opinion does not reflect any single one of these influences as it is established really as a combined effect.
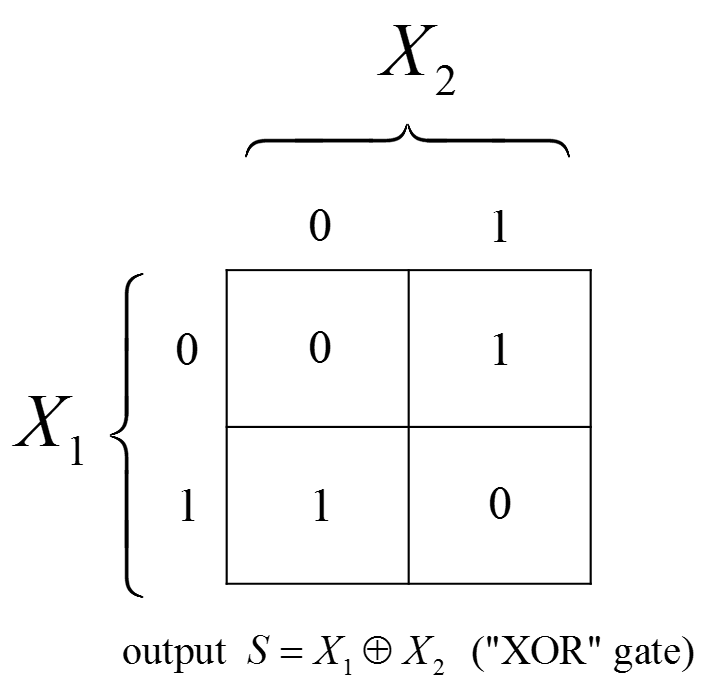
A simple illustration of synergy is depicted in the figure above. There are two independent input variables (X1 and X2), each of which can be either 0 or 1 with 50% probability. The output variable (S) is written in the cells of the table. We see that, a priori, S is distributed 50/50 over 0 and 1. It is easily verified that knowing only the input variable X1 tells us nothing about S: we know it is then 50/50 distributed but we knew this already. The same is true for X2. Only when we observe X1 and X2 simultaneously we can uniquely identify the output value S, implying perfect correlation.
Synergy is predominantly studied in the language of information theory. Information theory is the science of yes/no questions, quantified in units of bits. The stochastic variable X1 stores 1 bit of information because it requires minimally 1 yes/no question to identify its outcome ("is it 1?"). Similarly, X2 and S also store 1 bit each. Since S is fully determined by the two inputs it must be true that its 1 bit of information 'comes from' the inputs. We find that this 1 bit does not come from any individual input since after observing X1 we must still ask 1 yes/no question to determine the value of S, which is no better than before. Instead, the information in S has 'integrated' the input information: it stores whether the two inputs are equal or not (=1 yes/no question) but does not store the value of any individual input. In other words, S stores information about a higher-order function of the inputs instead of directly storing information from the inputs themselves.
The above example is trivial. As soon as the number of inputs grows beyond two, the number of permitted states per variable grows beyond two, and/or the inputs are not independent (so correlated amongst themselves) it remains an ongoing quest among information-theorists on how to define and quantify 'synergistic information'.
In our publication in Entropy we open up a completely new way of thinking about synergy. The currently dominating school of thought dates back to 2008 with the idea that synergistic information and individual information must sum up to the total amount of information. Although intuitive, unfortunately to date there seems to be no satisfactory axiom set and accompanying formula which has earned the consensus. Our proposal starts completely from scratch and departs from two very basic ideas: (1) that an output variable is fully synergistic when it stores zero information about any individual input; and (2) that a partially synergistic variable will correlate with a fully synergistic variable. Then we simply follow where the mathematics takes us. In the end we find a promising and well-defined formula for quantifying synergy. We can use it to prove various interesting things, such as the maximum amount of synergy that a fully synergistic variable can store about other variables. We feel it is a very promising path. Whether this new path leads to (part of) the solution remains to be seen.