2. Modelling in secondary education
2.3 Didactics of modelling
In educational practice it appears that many students have problems to carry out modelling activities with sufficient quality. Three important factors have been identified in various studies:1
- Lack of domain knowledge combined with modelling exercises in a too early stage of prior knowledge and skills;
- Insufficient understanding of the notion of model as a consequence of lack of attention to the required mathematical skills;
- Lack of understanding of the modelling process; students make little use of experiences with previous modelling activities.
Another factor is that translating a problem into a model (induction) and applying a model (deduction) are not equivalent in terms of comprehension. Induction leads from the special to the general and usually requires a greater creative effort than deduction from the general to the special.
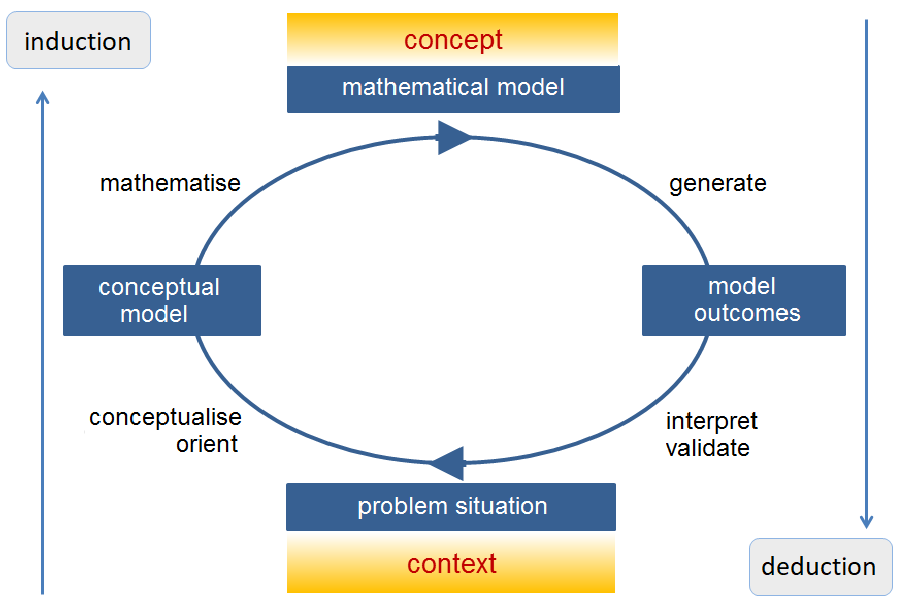
Fig 2.3 Inductive and deductive modelling activities
For the didactic implementation of the modelling cycle, it seems a good idea to separate the inductive and deductive modelling activities into two instructional elements with their own learning objectives:1
- Thinking in models
A modelling assignment starts with a question or problem, preferably linked to a demonstration or an experiment with a hands-on experience of the students (orientation). Then a first model or hypothesis is developed for the phenomenon under study (conceptualisation). The presumed relationships are translated into mathematical relationships, resulting into a mathematical or graphical model that can explain the observed facts or processes (mathematisation). - Working with
models
The model is analysed and simulated using mathematical methods that are often numerical or computational in nature and possibly require approximations (generation of results). By interpreting the model outcomes and comparing them with observations or experiments, the model is assessed (interpretation). Finally, the model is evaluated with regards to general aspects such as applicability and reliability, and adapted if necessary (validation).
In inductive modelling (thinking in models), students ideally develop their own models, that is, they are primarily expected to express and test their own ideas about the world. This brings special requirements on the didactics to be used for the modelling process to be carried out by students. In deductive modelling (working with models) students are not expected to apply and test their own ideas, but only a given model. These two forms of modelling are not contradictory but complementary. Both should play a role in a curriculum that aims to teach physics through modelling.2
The didactics of the modelling cycle, in particular the phase of model development, has important characteristics in common with inquiry-based learning and practical work at school. Effective practical work allows students to build a bridge between what they can see and do (hands-on) on the one hand and the explanatory scientific theories and models (brains-on) on the other hand.3 The principles of inquiry-based learning can therefore serve shaping modelling instruction in educational practice.4,5