3. Modelling learning path
3.4 Working with models
On this page and the page 3.3 Thinking in models we work out the Didactics of modelling into course elements that can that can occur in a particular order within the framework of a modelling task.1,2 The starting point in this guide is the order of activities that focus on modelling as presented in the modelling cycle: orientation, conceptualisation, mathematisation, generation of outcomes, interpretation, and validation.
The didactics of working with models (often referred to as 'modelling' in the teaching practice of secondary education) are more concrete in a number of distinct activities that match the attainment levels of the final examination in general secondary education (havo) and pre-university education (vwo).3,4 To illustrate the modelling activities, the subject of the subject of free fall in the school curriculum serves as one of the simplest examples of a dynamic model. In 4. Overview of models and model equations, more examples of dynamic models with corresponding files for the Coach 7 modelling environment5 are included.
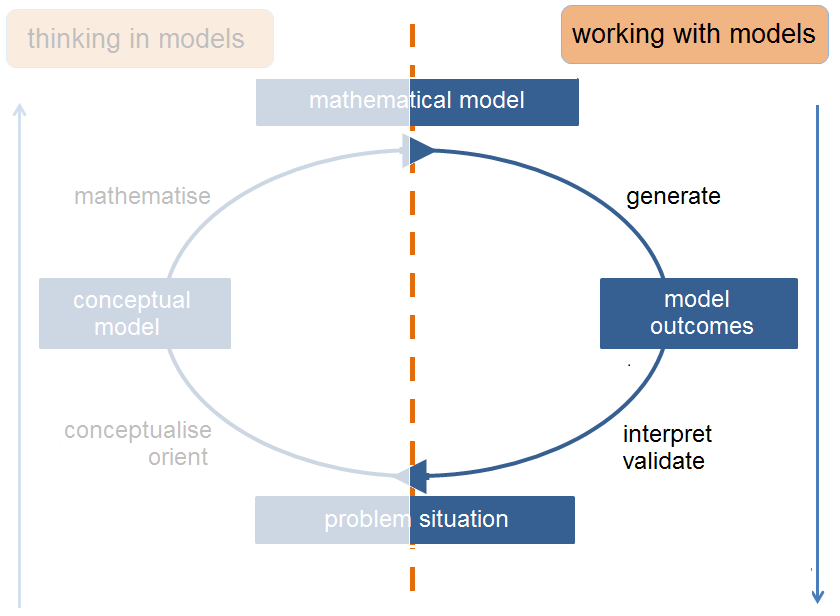
Fig 3.7 Working with models
- Elaboration
In order to be able to make quantitative statements, a conceptual model must be translated and elaborated in mathematical terms. This mathematisation is a crucial step in the modelling process. For this, students need to know what a 'variable' and what a 'formula' is. In more advanced assignments, students create a computer model. Usually a specific modelling environment will be used for this, such as Coach5 or Modellus.6 Model outcomes are generated with adequate initial values of the variables and model parameters.
Example: Free fall - Interpretation
In order to be able to interpret the model outcomes, it is important that testable expectations have been formulated about the behaviour of the model. It is important that students already have a number of mathematical skills such as being able to read and analyse graphs. They have to learn this at an early stage in order to be able to draw conclusions about the behaviour of various model variables on the basis of the shape of the graphs.
Example: Free fall - Validation
Without feedback to the problem or problem situation, the outcome of a model has little meaning. An important way to realise this feedback is to compare the model outcomes with the results of corresponding experiments or observations. For students whit more mathematical knowledge and skills, it is also possible to have the model results compare with the results of pencil-and-paper calculations for simplified situations.
Example: Free fall
In order to consolidate modelling as a way of thinking and a way of working, it is important to conclude a modelling task with a session in which students are encouraged to reflect on the results and the procedures followed. This explicitly structures insight into how modelling works. It increases the probability that students will work in a subsequent modelling assignment in a more structured way.1