3.2 Levels of modelling
Dynamic modelling: Free fall
A dynamic model describes the behaviour of a system in time and is characterised by the1
- initial state of the system;
- factors that influence the change of the state;
- time step in which the change takes place;
- recursive rule: new state := old state + change.
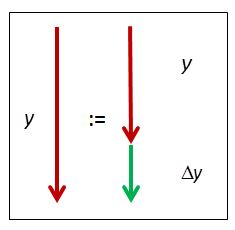
Fig 3.5 New position :=
old position + change
In the experiment to determine the acceleration of free fall, Table 1 provides a description of the falling motion divided into discrete time steps Δt. The state variables are the position y and the velocity v; change is determined by the gravitational acceleration g.
Based on the assumption that the acceleration of free fall is constant, Table 1 can be used to construct a dynamic model for computing the falling motion. In this model, the recursive rule for the compuration of the new state is
The change of the velocity per time step is obtained by reading off the formula from Table 1:
The change of velocity is obtained in a similar way
For given initial values of the position and the velocity, with these formulas, the falling motion of an object on which only the gravitational force works can be reconstructed step by step. With each subsequent time step, the change of position and velocity is computed and added to the previous state. The results can be compared with the measured data in Table 1.
Above, the transition actually takes place from the 'model of' free fall
(Table 1) to a mathematical 'model for' free fall. For students, this is a big conceptual
step that requires explicit attention in lessons. In textbooks, this conceptual step is often implicit in the explanation of the
computational model
of the motion of an object.2