Cumulative Distribution FunctionΒΆ

The cumulative distribution function brings the discrete and continuous RV’s toegether. For a RV \(X\) the cumulative distribution function (often called the distribution function) is defined as:

\[F_X(x) = \P(X\leq x)\]

Note that \(x\in\setR\) even in case \(X\) is a discrete RV. We have:

\[\begin{split}F_X(x) = \begin{cases} \sum_{k=-\infty}^{\lfloor x\rfloor} p_X(k) &\text{Discrete $X$}\\ \int_{-\infty}^{x} f_X(y)\, dy &\text{Continuous $X$} \end{cases}\end{split}\]

Below a probability mass function \(p_X\) is plotted and the corresponding \(F_X\).




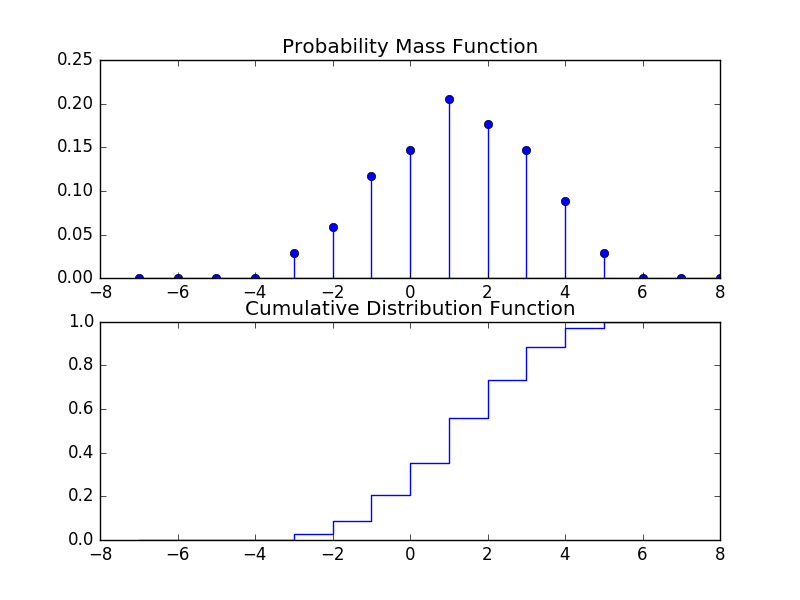
../../_images/discrete_cdf.png

And a plot of a probability density function and its corresponding
cumulative distribution function.





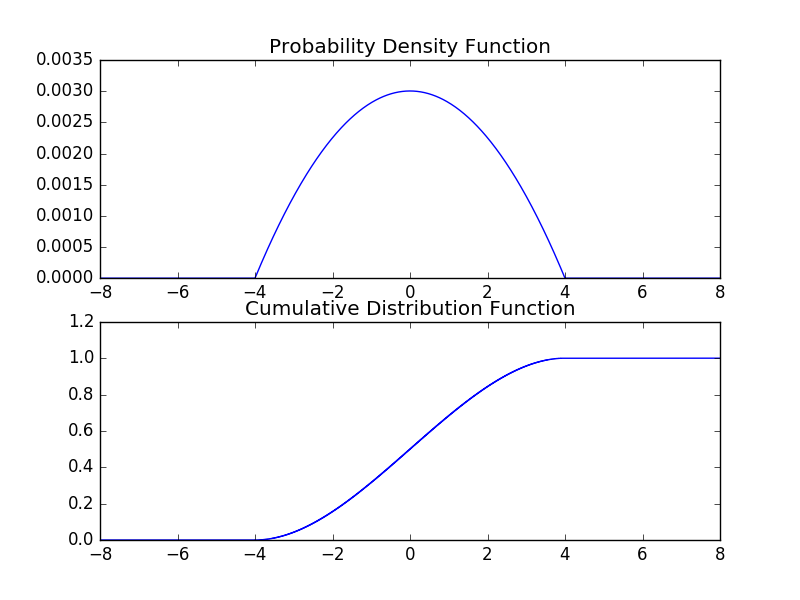
../../_images/continuous_cdf.png

The cumulative distribution function follows from the probability
density function by integration. We can go the other way as well:



\[f_X = \frac{d}{dx} F_X\]


With some mathematical leniency we could say that this also holds for
a discrete random variable.