Discrete Random Variables

A discrete random variable \(X\) maps the elementary events \(u\) in \(U\) unto a value in \(\setZ\). i.e. \(X: u\in U \mapsto X(u)\in\setZ\). Note that the random variable \(X\) in iteself is not an event. We can specify an event \(A\) by specifying

\[A = \{ u \bigm| X(u)=x \}\]

We will most often abbreviate this and write the event \(A\) as \(X=x\). Carefully note the distinction between capital \(X\) and \(x\). The capital \(X\) always refers to random variables and lower case letters refer to values from the range of the mapping \(X\).

A discrete variable is completely characterized in case for all \(x\in\setZ\) we specify \(\P(X=x)\). We will do this with the probability mass functions \(p_X\):

\[p_X(x) = \P(X=x)\]

As an example consider our fair dice again, there we have:

\[\begin{split}p_X(x) = \begin{cases} 0 &: x < 1\\ \frac{1}{6} &: 1\leq x \leq 6\\ 0 &: x > 6 \end{cases}\end{split}\]

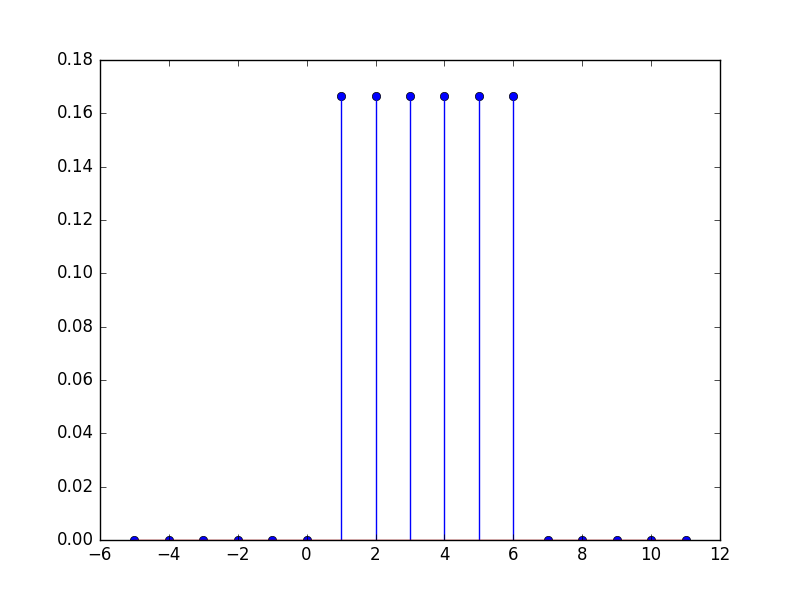
Note that we assume that the events \(X=x_1\) and \(X=x_2\) are disjunct in case \(x_1\not=x_2\) and futhermore that all \(X=x\) for \(x\in\setZ\) form a partition of \(U\) and therefore:

\[\sum_{x\in\setZ} p_X(x) = 1\]