5.3.2. Transforming Filters

\(\renewcommand{\w}{\omega}\)

5.3.2.1. Shifting Frequencies

We start with a first order low pass filter with transfer function:

\[H(s) = \frac{1}{s+1}\]

It’s frequency response is:

\[H(j\w) = \frac{1}{j\w+1}\]

and the absolute value:

\[|H(j\w)| = \frac{1}{\sqrt{\w^2+1}}\]

For \(\w\gg1\) we have \(\log|H(j\w)|-\log\w\) and for \(\w\ll1\) we have \(|H(\w)|=0\). The corner frequency thus is \(\w_c=1\).

We can shift the corner frequency to \(\w_c\) by substituting \(\w/\w_c\) for \(\w\), then:

\[H(j\w) = \frac{1}{j\frac{\w}{\w_c}+1}\]

In the \(s\)-domain we have:

\[H(s) = \frac{1}{\frac{s}{\w_c} + 1}\]

5.3.2.2. From Low to High Pass

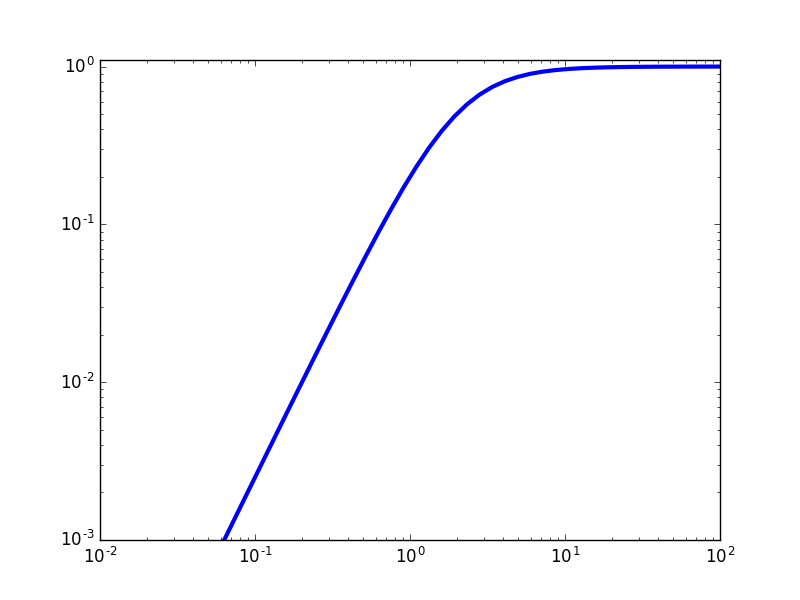
We start with a low pass filter with transfer function \(H(s)\). As a specific example we take:

\[H_{LP}(s) = \frac{1}{\tau s + 1}\]

This is a first order low pass filter. It’s frequency reponse is:

\[H_{LP}(j\omega) = \frac{1}{j \tau \omega + 1}\]

and the absolute value is:

\[|H(j\omega)| = \frac{1}{\sqrt{\tau^2 \omega^2 + 1}}\]

Plotting this frequency transform we get

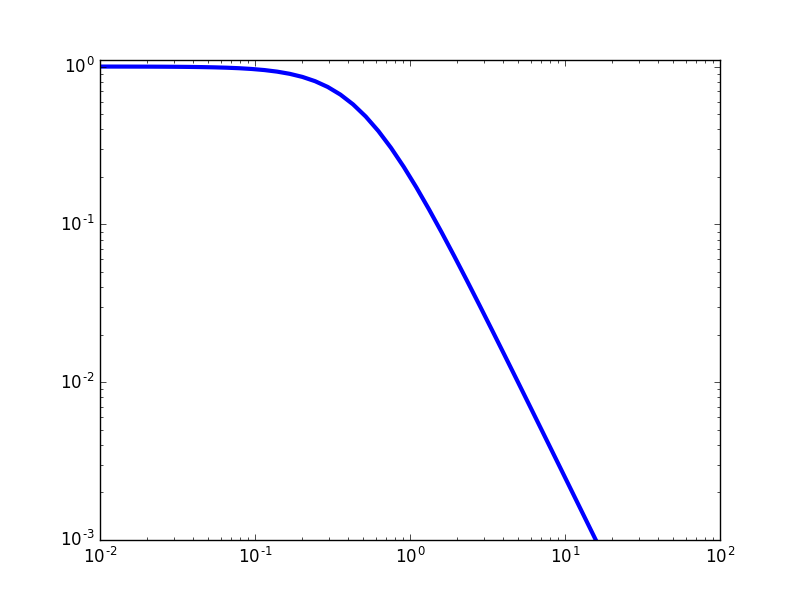
This simple low pass filter can be transformed to a high pass filter by substitution of \(j\omega\leftarrow1/(j\omega)\). Note that on a logarithmic scale for the frequencies we clearly see the inversion of the frequencies. So we get:

\[\begin{split}H_{HP}(j\omega) &= \frac{1}{\tau\frac{1}{j\omega}+1}\\ &= \frac{j\omega}{j\omega+\tau}\end{split}\]

Its frequency response (for \(\tau=1\)) is sketched below: