2. Modelling in secondary education
2.1 Learning modelling
Although modelling as a skill has been part of the physics attainment levels since 1991, modelling in the physics programme focuses primarily on dynamic modelling with difference question or differential equations, whether or not in the form of graphical modelling. Thinking in models, that is, model development as meant in the objectives of the havo1 and vwo2 exams, remains underexposed. This diminishes the meaning of the notion of model and modelling as a central component of physical theories, both in its development and its application.3
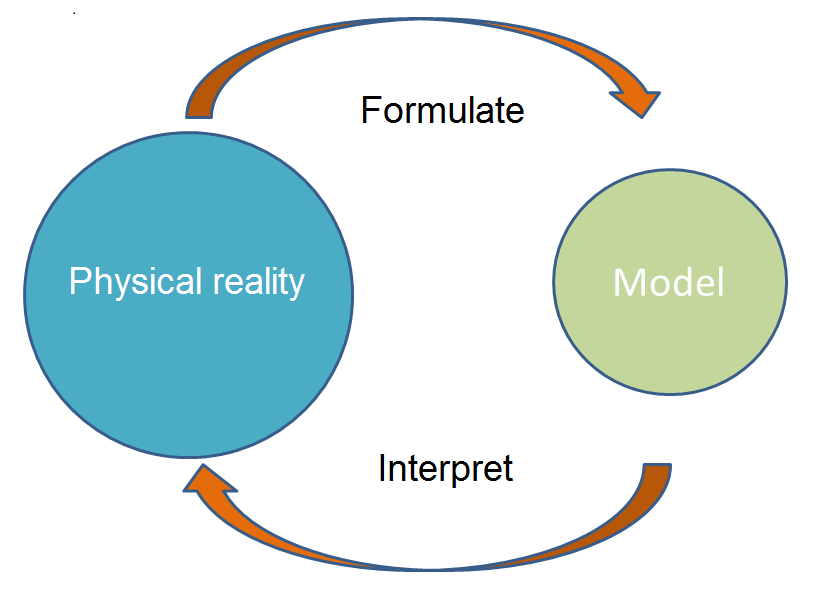
Fig 2.1 Modelling of a phenomenon or a system.
To emphasise the role of modelling in education, three central learning objectives can be distinguished:3,4
- Learning about models. Knowledge about the role and function of models in natural sciences as part of knowledge of the 'nature of science'. Students have insight into the relationship between a model and reality, and they can relate this to the applicability of the model;
- Learning modelling. Knowledge and skills of techniques for making, testing, and evaluating models. Students can construct models (only pre-university level [VWO]) and use them to describe, explain and predict properties and behaviour of systems;
- Learning domain content from a model. Models are always models of something. Their function is to better understand the modelled system or phenomenon. Students are able to compare and evaluate models of a specific phenomenon or system, and to adjust them on the basis of new data or new aspects.
In combination, these three learning objectives make it clear that modelling is not a separate subject in the curriculum, but rather consists of knowledge and skills that are used in all physics subjects (and in subjects of other natural sciences).
Such a ‘model curriculum’ can also contribute in practical terms to the quality of physics education. At this moment, the content is limited by the mathematical competencies of the students. Consequently, emphasis is on a small number of special or strongly simplified cases, and on momentary situations. The equations of motion themselves get out of sight. Through a systematic approach to modelling in education this can change:
- The limitations of mathematical computing become less restrictive and the repertoire to solve problems is enlarged. Models can be made with a considerably higher reality level, and dynamic processes, in which various quantities continuously change their value, can be studied;
- The fundamental equations take the central place in these models that they deserve. It offers students more opportunities to gain insight into the general character of the basic equations of physics.
This guide concerns the following questions: can the teaching of models, of the nature of models, and of modelling, not be integrated in a functional way in education, so that these goals reinforce each other? What does that mean for the role of the teacher? And how can the teaching of ‘learning modelling’ look in practice? 6,7