4. Geometrical Operators¶
An often used image operator is a geometrical operator, these are the operators that keep the colors the same but put the pixels in a different spot.
These operators can be used to create some artistical effect, but they are also useful in correcting for some unwanted distortion, which were introduced, when the picture was taken (like camera rotation, perspective distortions etc.)
The input for these methods (at least in this Exercise) is always a quadrilateral region of a discrete image \(F\). That means that you only know the intensity values at discrete integral pixel positions. The output consists of a rectangular image \(G\) with axes aligned with the Cartesian coordinate axes \(x\) and \(y\).
In an arbitrary image transformation, there is no guarantee, that an “input”-pixel will be positioned at a pixel in the “output” image as well. Rather, most of the time your output image pixels will “look at” image positions in the input image, which are “between” pixels.
So you need access to intensity values, which are not on the sampling grid of the original image, e.g. the intensitiy value at position \((6.4, 7.3)\). In this section we assume that you know about interpolation. Here we focus on the basic structure of an image warping algorithm.
Let \(f\) be an image with domain \(E\) and range \(V\). Let \(\phi\) be a transform that takes a point \(\v x\in E\) and returns a point \(\v y=\phi(\v x)\) in the domain \(E'\) of image \(g\), we then define the geometrical transform \(\Phi\) as:
or equivalently:
in case the inverse transform exists.
Note that the last two transforms are equivalent from a mathematical point of view. We could start an algorithm for a geometrical operator with either equation. We start with the first one:
4.1. Forward Transform¶
In [1]: from ipcv.ip.pixels import pixel, domainIterator;
In [2]: def geoOp_fwd(f, phi):
...: fdomain = f.shape[:2]
...: g = np.zeros_like(f)
...: for p in domainIterator(fdomain):
...: q = phi(p).rint()
...: if q.isin(fdomain):
...: g[q] = f[p]
...: return g
...:
The function geoOp2d_fwd is based on the first equation: we loop
over all pixels in the domain of image \(f\), calculate where that pixel
is transformed to and then set this pixel in the output image with the
same color as the original pixel in the original image.
Below we define a function that rotates a pixel and use it to rotate the entire image:
In [3]: def rotator(angle):
...: ca = np.cos(angle)
...: sa = np.sin(angle)
...: R = np.array([[ca, -sa], [sa, ca]])
...: def rotate(t):
...: return pixel(R @ np.array(t))
...: return rotate
...:
In [4]: a = plt.imread('images/peppers.png')
In [5]: plt.subplot(131); plt.imshow(a);
In [6]: b = geoOp_fwd(a, rotator(np.pi/6))
In [7]: plt.subplot(132); plt.imshow(b);
In [8]: plt.subplot(133); plt.imshow(b[:64,:64]);
In [9]: plt.show();
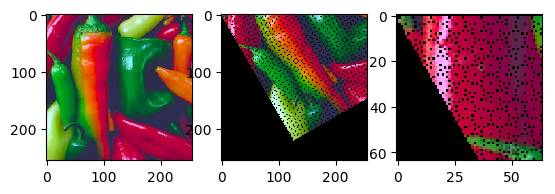
Evidently the forward transform is not the way to implement a geometrical transform. In the next sectio we will look at the backward transform that is based on the second formulation of the geometric operator.
4.2. Backward Transform¶
In [10]: def geoOp(f, invphi):
....: g = np.zeros_like(f)
....: gdomain = g.shape[:2]
....: for q in domainIterator(gdomain):
....: p = invphi(q).rint()
....: if p.isin(gdomain):
....: g[q] = f[p]
....: return g
....:
In [11]: plt.subplot(131); plt.imshow(a);
In [12]: b = geoOp(a, rotator(-np.pi/6))
In [13]: plt.subplot(132); plt.imshow(b);
In [14]: plt.subplot(133); plt.imshow(b[:64,:64]);
In [15]: plt.show();

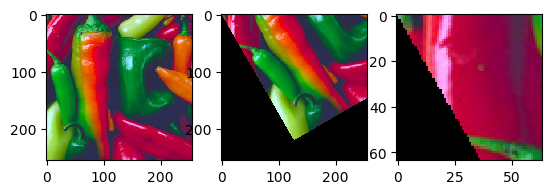
As can be clearly seen in this example the backward algorithm is the simplest one that really works. No more holes. Please note that we use a simple nearest neighbor interpolation. In practice it is much better to use a better interpolation scheme.
4.3. Geometrical Transform in Scikit-Image¶
The most generic form of a geometrical transform is called
skimage.transform.warp in skimage. As a second argument you have
to pass it the inverse transform. It can be a function that takes an
array of shape (M,2) of points in the result image and it should
return an array of the shape giving the positions of the corresponding
points in the input image. It is much like our geoOp function
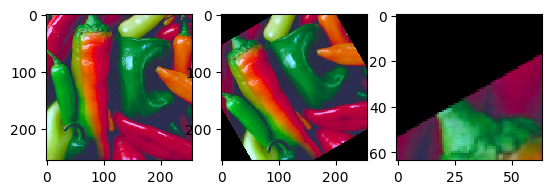
(only much faster). So let’s do the rotation again:
In [16]: from skimage.transform import warp
In [17]: def rotator_skimage(angle):
....: ca = np.cos(angle)
....: sa = np.sin(angle)
....: RT = np.array([[ca, -sa], [sa, ca]]).T
....: def rotate(x):
....: return x @ RT
....: return rotate
....:
In [18]: plt.subplot(131); plt.imshow(a);
In [19]: c = warp(a, rotator_skimage(np.pi/6))
In [20]: plt.subplot(132); plt.imshow(c);
In [21]: plt.subplot(133); plt.imshow(c[:64,:64]);
In [22]: plt.show();
Scikit-Image has several functions for specialized geometrical
transforms. In the example below we first set up the homogenuous
matrix that rotates around the center of an image and then instead of
using a callable as argument in warp we give it this matrix.
In [23]: def rotation_matrix(f, angle):
....: M,N = f.shape[:2]
....: T = np.array([[1, 0, M/2],
....: [0, 1, N/2],
....: [0, 0, 1 ]])
....: ca = np.cos(angle)
....: sa = np.sin(angle)
....: R = np.array([[ca, -sa, 0],
....: [sa, ca, 0],
....: [ 0, 0, 1]])
....: return T @ R @ np.linalg.inv(T)
....:
In [24]: plt.subplot(131); plt.imshow(a);
In [25]: d = warp(a, rotation_matrix(a, np.pi/6))
In [26]: plt.subplot(132); plt.imshow(d);
In [27]: plt.subplot(133); plt.imshow(d[:64,:64]);
In [28]: plt.show();
4.4. Geometrical Transforms in OpenCV¶
OpenCV also has a lot of geometrical transform algorithms. Here we
only discuss warpPerspective to implement the image rotation
around the center.
In [29]: from cv2 import warpPerspective
In [30]: def rotation_matrix(f, angle):
....: M,N = f.shape[:2]
....: T = np.array([[1, 0, M/2],
....: [0, 1, N/2],
....: [0, 0, 1 ]])
....: ca = np.cos(angle)
....: sa = np.sin(angle)
....: R = np.array([[ca, -sa, 0],
....: [sa, ca, 0],
....: [ 0, 0, 1]])
....: return T @ R @ np.linalg.inv(T)
....:
In [31]: plt.subplot(131); plt.imshow(a);
In [32]: M = rotation_matrix(a, np.pi/6)
In [33]: e = warpPerspective(a, M, dsize=a.shape[:2])
In [34]: plt.subplot(132); plt.imshow(e);
In [35]: plt.subplot(133); plt.imshow(e[:64,:64]);
In [36]: plt.show();
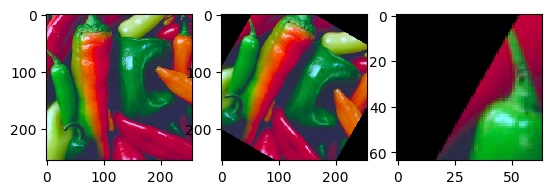
That seems to work, doesn’t it. But notice that the rotation is clockwise in this case whereas in the previous examples the rotation was counter clockwise. This is due to the fact that we have been specifying our rotation matrix with respect to the indices axis of the image, i.e. first axis from top to bottom and second axis from left to right. OpenCV uses the xy axis where x runs from left to right and y runs from top to bottom.
Because we are rotation around the center of the image we don’t notice the error in specifying the center of the image.
The easy way to get the correct rotation matrix is to reverse the sign of rotation angle but that is only a solution for a rotation matrix of course. Consider a \(3\times3\) homogeneous matrix used in the transform:
Compare this with:
What should be the new matrix? Can you fill in the dots? An easy way to do this is to note that
Can you prove that the matrix we are looking for then is given by \(F M F\) where \(F\) is the matrix that flips the coordinates and \(M\) is the original matrix.
Furthermore when specifying image sizes in OpenCV the tuple dsize
is (cols, rows), again first specify the horizontal size, then the
vertical size (and note that is not what is done in the code...)

