1.2.1. Plotting Signals

\(\newcommand{\setR}{\mathbb R}\) \(\newcommand{\setC}{\mathbb C}\)

1.2.1.1. Plotting Real Values Signals

Consider a CT signal \(x(t)\). A real valued CT signal is plotted using the standard ways to plot a function \(x: \setR \rightarrow \setR\). Consider the sinusoidal signal \(x(t)=325 \sin(2\pi 50 t)\) for a short interval of time we can plot this as:

In [1]: t = np.linspace(-0.02, 0.05, 1000)

In [2]: plt.plot(t, 325 * np.sin(2*np.pi*50*t));

In [3]: plt.xlabel('t');

In [4]: plt.ylabel('x(t)');

In [5]: plt.title(r'Plot of CT signal $x(t)=325 \sin(2\pi 50 t)$');

In [6]: plt.xlim([-0.02, 0.05]);

In [7]: plt.show()

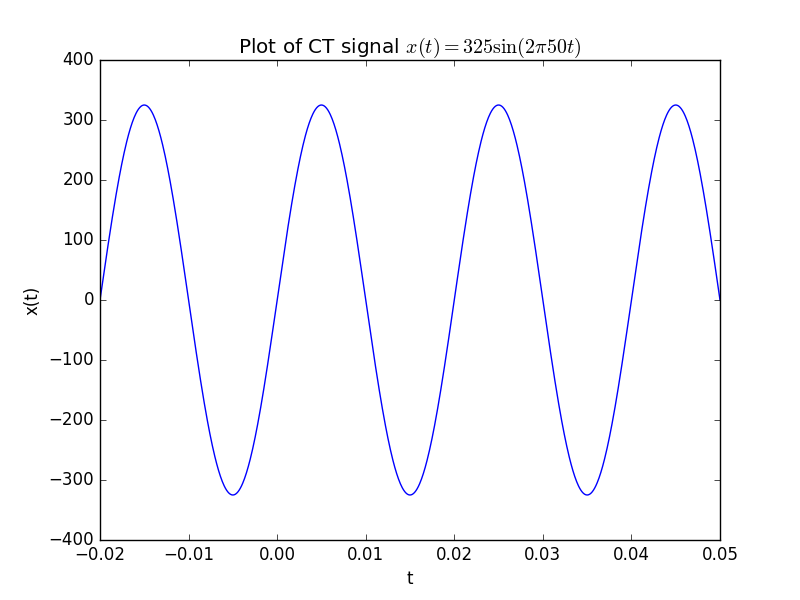
Evidently the above plot is a lie. You cannot plot a CT signal on a digital device. In Computer Graphics class you have or will learn that a function (signal) is plotted as a chain of straight lines (and even the straight lines are discretized as a set of dots). But it sure looks like a CT signal doesn’t it?

Things are different when we consider a DT signal. Given the values of \(x[n]\) for say \(n=0\) to \(n=100\) we could use the same strategy and plot it as we did for the CT signal: just connect the dots \((n, x[n])\). That is done in practice often. However in these notes when dealing with the differences between CT and DT signals we want to stress that a DT signal essentially is just a sequence of numbers. There is no need to think about \(x[n+0.2]\) in the discrete domain and certainly no need to visualize it.

Therefore a DT signal is plotted as a sequence of vertical bars. A stem plot:

In [8]: n = np.arange(50);

In [9]: dt = 0.07/50

In [10]: x = np.sin(2 * np.pi * 50 * n * dt)

In [11]: plt.xlabel('n');

In [12]: plt.ylabel('x[n]');

In [13]: plt.title(r'Plot of DT signal $x[n] = 325 \sin(2\pi 50 n \Delta t)$');

In [14]: plt.stem(n, x);

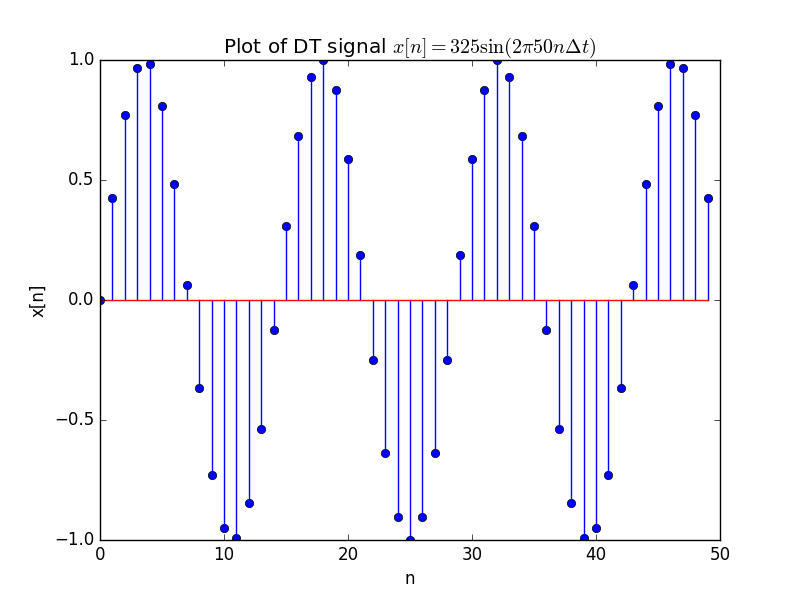
1.2.1.2. Plotting Complex Valued Signals

Now consider the complex valued CT signal:

\[x(t) = e^{j 100 \pi t}\]

Plotting such a signal as if it were a real valued signal results in a Python warning that complex numbers are casted to real by discarding the imaginary parts. To see everything we have to plot both the real and imaginary part of the signal.

In [15]: t = np.linspace(-0.02, 0.05, 1000)

In [16]: plt.subplot(2,1,1); plt.plot(t, np.exp(2j*np.pi*50*t).real );

In [17]: plt.xlabel('t');

In [18]: plt.ylabel('Re x(t)');

In [19]: plt.title(r'Real part of  $x(t)=e^{j 100 \pi t}$');

In [20]: plt.xlim([-0.02, 0.05]);

In [21]: plt.subplot(2,1,2); plt.plot(t, np.exp(2j*np.pi*50*t).imag );

In [22]: plt.xlabel('t');

In [23]: plt.ylabel('Im x(t)');

In [24]: plt.title(r'Imaginary part of  $x(t)=e^{j 100 \pi t}$');

In [25]: plt.xlim([-0.02, 0.05]);

In [26]: plt.show()

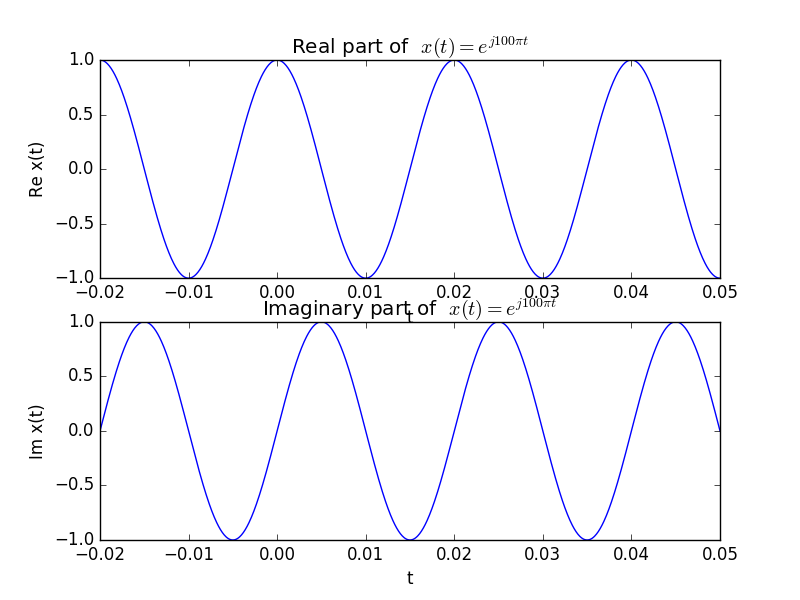
Instead of plotting the real and imaginary part of a complex signal, we can also plot the magnitude and angle of the complex values.

In [27]: t = np.linspace(-0.02, 0.05, 1000)

In [28]: plt.subplot(2,1,1); plt.plot(t, np.abs(np.exp(2j*np.pi*50*t)) );

In [29]: plt.xlabel(r'$t$');

In [30]: plt.ylabel(r'$|x(t)|$');

In [31]: plt.title(r'Absolute value  of  $x(t)=e^{j 100 \pi t}$');

In [32]: plt.xlim([-0.02, 0.05]);

In [33]: plt.subplot(2,1,2); plt.plot(t, np.angle(np.exp(2j*np.pi*50*t))*360/(2*np.pi) );

In [34]: plt.xlabel('$t$');

In [35]: plt.ylabel(r'$\angle x(t)$');

In [36]: plt.title(r'Phase of  $x(t)=e^{j 100 \pi t}$');

In [37]: plt.xlim([-0.02, 0.05]);

In [38]: plt.show()

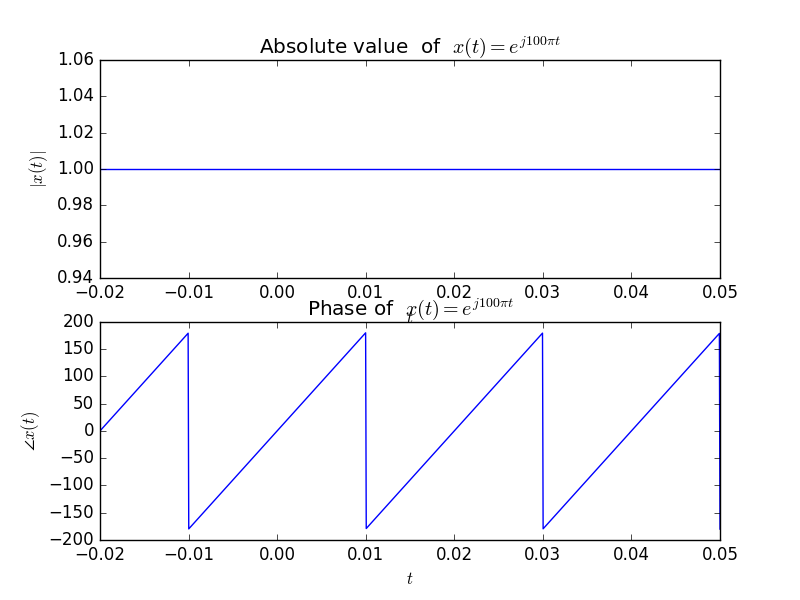
Note that both plots of the complex signal are equivalent. They both do represent the same signal. Also note the seemingly strange behaviour of the phase (angle) plot. It looks quite discontinuous. But it is really not because the phase jumps from +180 degrees to -180 degrees and that is of course the same angle! This phenomenon will be seen quite a lot when plotting the phase of complex signals and functions. It is called phase wrapping. If we would allow angles outside the range from -180 to +180 we could obtain a perfectly straight line (doing just that is called phase unwrapping).