3. Modelling learning path
3.2. Levels of modelling
A modelling learning path can be structured over time through a choice of modelling tasks with increasing degree of difficulty. Four modelling levels can be distinguished that elaborate on each other:1,2
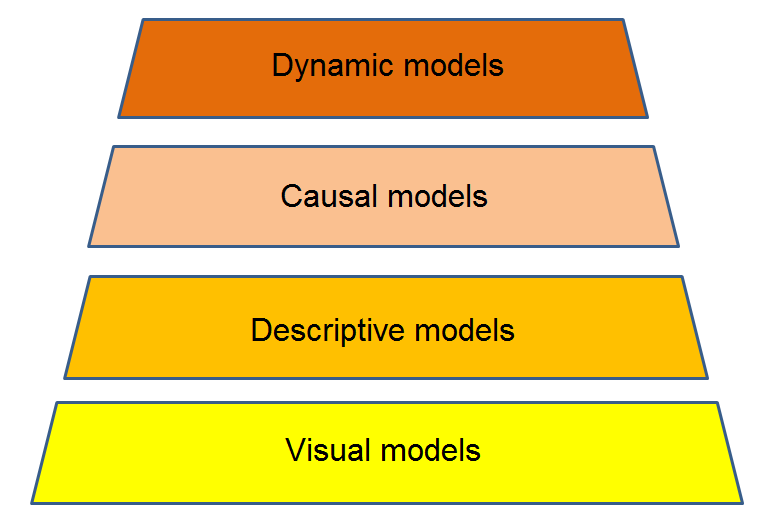
Fig 3.2 Modelling levels at increasing degree of abstraction
- Visual modelling
Conceptualisation with the help of models can start al lower secondary level with what pupils already know and can do. At this ‘common sense’ level, models are often of visual nature and the concept of model has the meaning of a simplified, often geometrical, representation of physical reality.
Example: Drawing-based modelling - Descriptive modelling
A more scientific way of modelling starts with the development of descriptive models consisting of variables with relations between them, represented in the form of discrete tables and graphs. The function of the model as an aid in the understanding of phenomena takes precedence over the resemblance to the object of research.
Example: Falling motion - Causal modelling
A next step is taken towards models that give a causal explanation of the described processes in terms of an underlying mechanism. This includes a transition from discrete to continuous variables and the associated mathematical functions and formulas.
Example: Quantum particle - Dynamic modelling
In principle, the causal mechanisms also lead to explanations and/or predictions of dynamic systems, that is, of systems in which time plays an important role. Dynamic modelling is mentioned here as a separate category because this type of models usually cannot be elaborated analytically. For solving dynamic systems, additional numerical and computational skills are required.
Example: Dynamic model
The task is to bring students in secondary education to level four. Such a learning objective requires constant attention during a long-term educational program. In general secondary education (havo) and pre-university education (vwo), modelling can begin at the visual and descriptive level, possibly supported by a modelling tool such as SimSketch. A good embedding in the curriculum requires that modelling is not treated as an isolated subject within a single course, but that modelling is a recurring subject which is taught in substantive collaboration and coordination between the science subjects.3
Such a development only has a chance of success if it has broad support in secondary education, and if teachers also have the required didactic repertoire. Especially the transition from model of (level 1) to model for (level 2) is not easy, takes time and only takes place if attention is shifted explicitly from the context to the involved mathematical relations.4 In this transition, the teacher plays a crucial role by actively supporting the most difficult abstraction steps, which are often underexposed in teaching methods5, through appropriate work formats.