6.4.1. Neural Networks: the Third Revolution

Fig. 6.4.5 McCulloch Pitts model of a human neuron.

Yes indeed we are in the middle of the third neural network revolution. The first one was in the forties when McCullogh and Pitts came with a simplified model of a human neuron. Their analysis was based on classical logic but unfortunately there was no learning algorithm known for the model.

In the mid fifties Rosenblatt proposed the perceptron. Each neuron was essentially a logistic regression classifier albeit it with a non differentiable activation function.

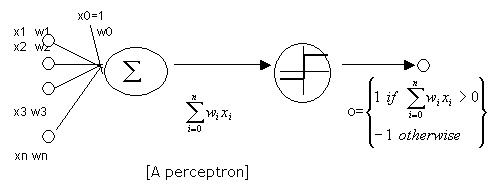
Fig. 6.4.6 The Perceptron neuron model. Note that the target values were either -1 and +1.

Rosenblatt came up with a learning rule that is close to the learning rule of the logistic classifier although their rule was only guaranteed to converge to a solution in case the learning set was indeed linear separable. Rosenblatt even made a hardware implementation of the perceptron that was able to learn to recognize visual patterns (of size \(20\times20\)).

In 1960 Widrow and Hoff proposed the ADALINE (adaptive linear neuron). In the running phase it performed just like the perceptron. But in the learning phase the non linear activation function was not used, only the linear summation part. This lead to linear regression model and learning rule. The ADALINE learning rule is known as LMS (least mean squares) rule, or as the Widrow-Hoff rule or simple as the delta rule. A three layer network based on ADALINE was called MADALINE and there were in fact learning rules for these networks (including one that was proven later to be the backpropagation rule, for that network the activation function was indeed the sigmoid function).

Fig. 6.4.7 The cover of the (extended) version of the book Perceptrons

Then at the end of the sixties, Minsky and Papert wrote a famous book: “Perceptrons”. They criticized perceptrons by investigating the limitations of networks. They showed that a one neuron perceptron could not solve the XOR problem. They knew it could be done with an extra layer but at the time there was no learning algorithm to derive the parameters by learning. This book started the “winter of neural networks”, very few scientists dare upon touching the subject as these two famous scientists decided that perceptrons were fundamentally flawed.

Minsky’s and Papert’s research went much further that just the XOR problem. They showed that not even a (finite) multi layer network of perceptrons can decide upon the connectivity of sets (as inputs they considered binary images just like the classical perceptron). This is what is illustrated on the cover of their book. You might think that both red drawings are one line. But in fact one drawing shows one red line and the other shows two red lines. The human visual brain is topoagnostic as well (at least i don’t know anyone that is capable of seeing the difference between the two drawings at once).

Then in the eighties things got better for the neural network afficionado. The backpropagation algorithm was discovered. And as with many important ideas this one has many fathers as well. Dreyfuss, Werbos and Rumelhart are often cited to be one of the fathers of backpropagation.

Backpropagation essentially is the way to learn all the parameters in a feed forward network of simple perceptron neurons. With the important change that the activation function was chosed to be the sigmoid function: a differentiable function. Backpropagation through a modern looking glass is nothing else then a clever way of using the chain rule of differentation.

Backpropagation marked the start of the second revolution of neural networks. But interest decreased over time. Neural networks did not significantly outperform methods that we more firmly grounded on statistical theory. It was (and is) hard to really explain what a neural network is doing; in what way it comes to its decisions. Support vector machines became the machine learning tool of choice in the ninetees and beginning of the 21st century.

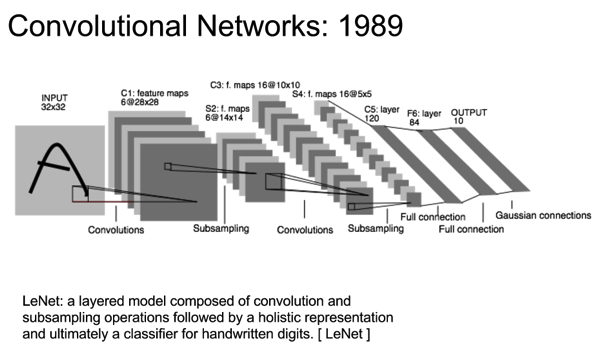
Fig. 6.4.8 LeNet. Deep learning network based on convolutions for letter and digit recognition

Neural networks were still being used though and most notably (especcially in hindsight) Le Cun et al basically reinvented the neocognitron of Fukushima (1980) but added the backpropagation learning in LeNet (1989) the first deep learning network based on convolutions for letter and digit recognition. This architecture still is much like modern days deep learning network architectures.

With the increase of computer power, availabilty of advanced tools (like automatic differentiation) and development of powerful extentions of the classical gradient descent optimization, deep learning architectures with tens and even hundreds of (convolutional) layers became popular and the results are spectacular.

Yes we are indeed witnessing the third revolution of neural networks.