1.4. The Chain Rule of Differentiation

1.4.1. A chain of functions

Consider the functions \(f\), \(g\) and \(h\). We consider the chain composition of these functions \(h\after g\after f\) defined as:

\[y = k(x) = (h\after g\after f)(x) = h(g(f(x)))\]

In a flow graph the function composition is sketched in Fig. 1.4.1.

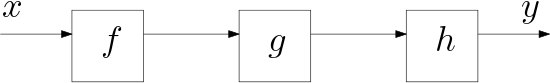
../../_images/hogof.png

Fig. 1.4.1 Flow graph of the function composition \(h\after g\after f\)

1.4.2. The Chain Rule

Let’s start with the composition of two functions:

\[h(x) = (g\after f)(x) = g(f(x))\]

When we differentiate a function we are looking at the change in the function value as a consequence of an infinitesimal change in the independent variable \(x\). We have in first order:

\[h(x+dx) = h(x) + h'(x) dx\]

Now we do the same for \(h(x)=g(f(x))\):

\[\begin{split}h(x+dx) &= g(f(x+dx))\\ &= g(f(x)+f'(x)dx)\\ &= g(f(x)) + g'(f(x))f'(x)dx\\ &= h(x) + g'(f(x)) f'(x) dx\end{split}\]

Comparing both expressions for \(h(x+dx)\) we get:

\[h'(x) = g'(f(x)) f'(x)\]

the familiar chain rule that all of us learned at high school.

The derivative of the composed function \(k = h\after g\after f\) is given by the chain rule

(1.4.1)\[\frac{dk}{dx} = (h\after g\after f)'(x) = h'(g(f(x))\;g'(f(x))\; f'(x)\]

This is easily proved given the chain rule for the composition of two functions.

In functional terms we can write:

\[(h\after g\after f)' = (h'\after g \after f)\;(g'\after f)\;f'\]

where the multiplication of functions like \(f g\) is defined as \((fg)(x)=f(x)g(x)\).

1.4.3. The Leibnitz Notation

Consider again the function composition

\[(h\after g\after f)(x) = h(g(f(x)))\]

If we define \(u = f(x)\) and \(v = (g\after f)(x)\) and indicate the values in the flow graph (see Fig. 1.4.2)

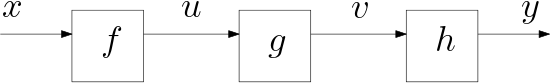
../../_images/hogof_uv.png

Fig. 1.4.2 Flow graph of the function composition \(h\after g\after f\) with intermediate value.

The derivative of the composed function is:

\[(h\after g\after f)'(x) = h'(v) g'(u) f'(x)\]

or equivalently:

\[\frac{dy}{dx} = \frac{dy}{dv} \frac{dv}{du} \frac{du}{dx}\]

From here the traditional Leibnitz notation gets a bit sloppy, confusing at the start but convenient once you get used to it. Instead of using a new symbol for the result of a function in the chain (in our example \(u=f(x)\) and \(v=g(f(x))\)) we will use the function names for its output value as well. The chain rule in Leibnitz form then becomes:

\[\frac{dh}{dx} = \frac{dh}{dg}\;\frac{dg}{df}\;\frac{df}{dx}\]

In summary: for every node (function) in the chain we diffentiate the output with respect to its input. And multiplying these ‘one-function-derivatives’ we can calculate the derivative of (part of) the chain.

1.4.4. Multivariate Chain Rule

In the machine learning context we will be using the chain rule a lot for multivariate functions. Consider a simple one

\[f(u, v)\]

We will look at how the value of \(f\) will change if both \(u\) and \(v\) change a small bit, say from \(u\) to \(u+du\) and from \(v\) to \(v+dv\). The change \(df\) in \(f\) then is:

\[df = f(u+du, v+dv) - f(u, v)\]

Note that in the univariate case we have

\[f(x+dx) = f(x) + f_x(x) dx\]

if we now only consider the change in \(u\) and keep the second argument constant we get:

\[df = f(u, v+dv) + f_u(u, v+dv) du - f(u,v)\]

Now for both terms we keep \(u\) constant and apply the same line of reasoning to the second argument of \(f\) we get:

\[\begin{split}df &= f(u,v) + f_v(u,v)dv + (f_u(u,v) + f_{uv}(u,v)dv)du - f(u,v)\\ &= f_u(u,v)du + f_v(u,v)dv + f_{uv}(u,v) du dv\end{split}\]

Note that \(dudv\) is neglible small when compared with both \(du\) and \(dv\) and thus within first order:

\[df = f_u(u,v) du + f_v(u,v) dv\]

This is called the total derivative of \(f\). The above is an intuitive introduction of the concept but it can be given a solid mathematical foundation. The total derivative states that the change of \(f\) is the sum of the contributions due to the changes in its arguments.

Now we consider the situation where both \(u\) and \(v\) are functions of \(x\). Then we have

\[\begin{split}df &= f_u(u(x), v(x)) du(x) + f_v(u(x),v(x))dv(x)\\ &= f_u(u(x), v(x)) u_x(x) dx + f_v(u(x),v(x)) v_x(x) dx\end{split}\]

and thus

\[\frac{df}{dx} = f_u(u(x), v(x)) u_x(x) + f_v(u(x),v(x)) v_x(x)\]

or in Leibnits notation:

\[\frac{df}{dx} = \pfrac{f}{u} \frac{du}{dx} + \pfrac{f}{v} \frac{dv}{dx}\]

In general for a function \(f\) with \(n\) arguments each depending on \(x\):

\[g(x) = f(u_1(x),\cdots,u_n(x))\]

we have:

\[g'(x) = \sum_{i=1}^n f_{u_i}(u_1(x),\cdots,u_n(x)) u_i'(x)\]

Or in Leibnitz notation

\[\frac{dg}{dx} = \sum_{i=1}^n \pfrac{f}{u_i} \frac{du_i}{dx}\]

And finally if we are given a multivariate function \(f\) whose \(n\) arguments all depend on \(m\) arguments \(x_1,\ldots,x_m\), i.e.

\[g(x_1,\ldots,x_m) = f(u_1(x_1,\ldots,x_m),\ldots,u_n(x_1,\ldots,x_m)),\]

we get

\[\pfrac{g}{x_j} = \sum_{i=1}^n \pfrac{f}{u_i} \pfrac{u_i}{x_j}\]

This last expression is of great importance in the machine learning context.

1.4.5. Exercises

  1. Chain rule for the composition of more then two functions

    Given the chain rule for the composition of two functions:

    \[(g\after f)'(x) = g'(f(x))\;f'(x)\]

    or equivalently in functional notation

    \[(g\after f)' = (g'\after f)\; f'\]

    1. Give a proof for the derivative of the composition of three functions, i.e. give a proof for Eq.1.4.1.

    2. Now consider the function composition \(y = (f_n\after f_{n-1} \after\cdots\after f_1)(x)\). Give the derivative of \(y\) with respect to \(x\) of this function chain using the Leibnitz notation.

  2. Leibnitz notation for the chain rule

    Consider the function

    \[y = \log(\cos(x^2))\]

    can be written as the composition

    \[y = (f\after g\after h)(x)\]

    1. Identify the three functions \(f\), \(g\) and \(h\).

    2. Set \(y = f(u)\), \(u = g(v)\) and \(v = h(x)\) and calculate \(d y/ dx\) using the Leibnitz convention.