2.2. Conditional Probabilities
The conditional probability \(\P(A\given B)\) is the probability for event \(A\) given that we know that event \(B\) has occured too. For example we may ask for the probability of throwing a 6 with a fair die given that we have thrown an even number of points.
The conditional probability of \(A\) given \(B\) is:
In practical applications in machine learning we find ourselves in the situation were we would like to calculate the probability of some event, say \(\P(A)\), but only the conditional probabilities \(\P(A\given B)\) and \(\P(A\given \neg B)\) are known. Then the following theorem can be used.
The proof starts with observing that:
and because \(A\cap B\) and \(A\cap \neg B\) are disjunct we may apply the third axiom and obtain:
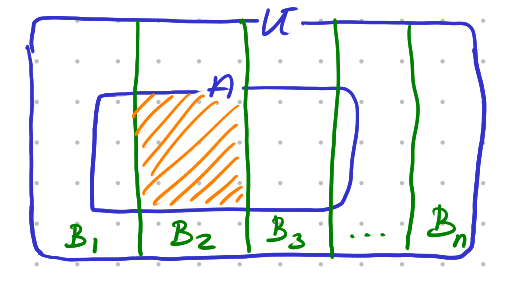
Fig. 2.2.1 Law of Total Probability. The hatched area indicates the set \(A\cap B_2\).
This theorem may be extended to partitions of the universe \(U\). A partition of \(U\) is a collection of subsets \(B_i\) for \(i=1,\ldots,n\) such that \(B_i \cap B_j=\emptyset\) for any \(i\not=j\) and \(B_1\cup B_2\cup\cdots\cup B_n=U\) .
For any partition \(\{B_i\}\) of \(U\) we have:
The proof is a generalization of the proof for the partition \(\{B, \neg B\}\).
Bayes rule allows us to write \(\P(A\given B)\) in terms of \(\P(B\given A)\):
The proof of Bayes rule simply follows from the definition of the conditional probability.
The definition of the conditional probability can be written in another form:
In this form it is known as the chain rule (or product rule). This rule can be generalised as: