2.3. Probability Trees

When you have learned to make probability trees in high school you have used conditional probabilities and the chain rule probably without knowing it. Consider the following random experiment. There are two vases labelled \(V_1\) and \(V_2\). In the vases are marbles of three colors. The following table shows how many of each color are in the vases.

Vase	#Red	#Green	#Blue
1	2	3	4
2	3	5	1

First we randomly select a vase (no preference for a vase) and then from the selected vase we pick a marble. The probability tree looks like:

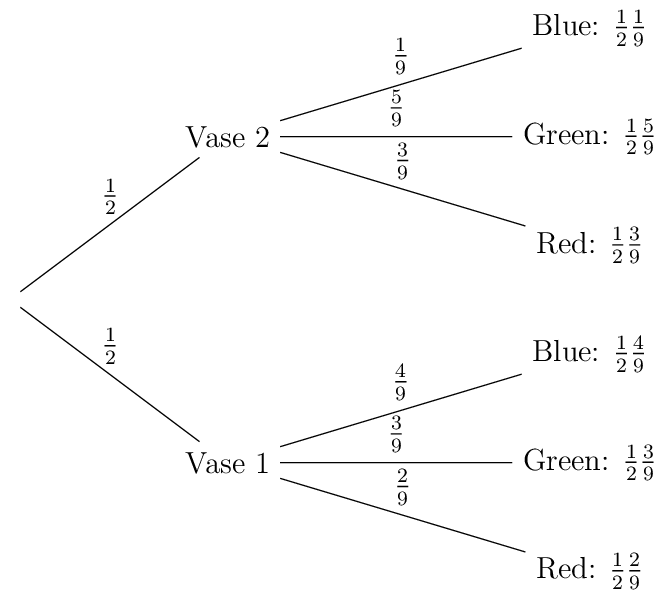
Starting at the root node on the left we first select Vase 1 or Vase 2. From either the node ‘Vase 1’ or the node ‘Vase 2’ we then pick a marble from the vase. The marble is either ‘Red’, ‘Green’ or ‘Blue’.

The probability of picking either vase is \(1/2\) . Picking a Red marble from Vase 1 has probability \(\P(\text{Red}\given \text{Vase 1})=2/9\) . So the probability of ending up with a Red marble from Vase 1 is given by:

\[\P(\text{Vase 1}\cap \text{Red}) = \P(\text{Vase 1}) \, \P(\text{Red}\given \text{Vase 1}) = \frac{1}{2}\,\frac{2}{9}\]

Thus the ‘trick’ that you have been using in highschool to multiply the probablities along the edges in the tree is nothing else then the application of the chain rule of conditional probabilities.