\(\newcommand{\in}{\text{in}}\) \(\newcommand{\out}{\text{out}}\) \(\newcommand{\prt}{\partial}\) \(\newcommand{\fracprt}[2]{\frac{\prt #1}{\prt #2}}\)

6.4.3.3. Activation Block

Consider a network of two linear layers. Let \(\v x\) be the input and \(\v y\) be the output of the first layer and input to the second layer. The total output \(\v z\) of the two layers is given by:

\[\v z = W_2 ( W_1 \v x + \v b_1) + \v b_2\]

It is because of the linearity that

\[\v z = W \v x + \v b\]

where \(W = W_2 W_1\) and \(\v b = W_2 \v b_1 + \v b_2\). So a neural network with only linear units doesn’t need hidden layers as it always will act like one layer.

Therefore a non linear activation function is inserted. One layer then functions as

\[\v y = g\aew( W\v x + \v b)\]

Note the use of \(g\aew\) to indicate the elementwise application of the function \(g\) to all elements in a vector (or matrix). It is this strange operator in the linear algebra context that will be the cause for some strange looking formula’s in the back propagation procedure.

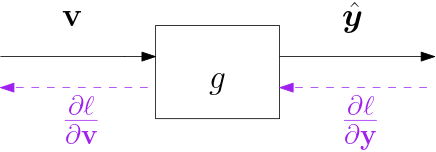
Fig. 6.4.17 Activation Block \(\v y = g\aew(\v v)\)

But first we concentrate on the activation function itself:

\[\v y = g\aew(\v v)\]

where we write \(g\aew(\v v)\) (note the dot) to indicate the element wise application of the function \(g\), i.e. \(y_i = g(v_i)\) for all \(i\).

For the derivative of the loss with respect to the input vector we have to remember that

\[y_i = g(v_i)\]

and thus

\[\pfrac{\ell}{v_i} = \pfrac{\ell}{y_i}\pfrac{y_i}{v_i} = g'(v_i)\pfrac{\ell}{y_i}\]

The vector \(\prt\ell/\prt v\) then is the element wise multiplication of the vector \(g'\aew(\v v)\) and \(\prt\ell/\prt\v y\). Standard linear algebra has no concise notation for that. In the ML literature the operator \(\odot\) is used for that purpose:

\[\pfrac{\ell}{\v v} = g'\aew(\v v) \odot \pfrac{\ell}{\v y}\]

Element wise multiplication is of course easy to do in Numpy, but very special in linear algebra (it is not linear of course).

In modern days use of neural networks it is especcially the ReLu activation function that is used quite often. We refer to the Wikipedia page on activation functions for a nice overview of a lot of different activation functions. That page tabulates both the expressions for the activation function \(g\) but also the expression for the derivative. Implementation in Python/Numpy should be easy from there.

The vectorized expression for batches \(V\) and \(Y\) is:

\[\pfrac{\ell}{V} = g'\aew(V) \odot \pfrac{\ell}{Y}\]

where the activation function is applied elementwise to all elements in the matrix \(V\) and is element wise multiplied with the matrix \(\pfrac{\ell}{Y}\).