\(\newcommand{\in}{\text{in}}\) \(\newcommand{\out}{\text{out}}\) \(\newcommand{\prt}{\partial}\)

6.4.3.2. Bias Block

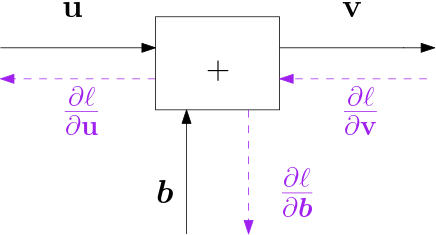
Fig. 6.4.16 Bias Block \(\v v = \v u + b\)

The forward pass of the bias block is simple:

\[\v v = \v u + \v b\]

The graph for this block is given in Fig. 6.4.16.

it simply adds a vector \(\v b\) to the input. Evidently this block passes the the derivative of \(\ell\) with respect to its output directly to its input:

\[\pfrac{\ell}{\v u} = \pfrac{\ell}{\v v}\]

and also to the parameter vector:

\[\pfrac{\ell}{\v b} = \pfrac{\ell}{\v v}\]

we leave the proofs as exercises for the reader (again the easiest way to do so is by considering all elements of the vectors).

The vectorized expressions are:

\[V = U + \v 1 \v b\T\]

note that \(\v 1\v b\T\) constructs a matrix in which all the rows are \(\v b\T\). And also note that Numpy is smart enough to broadcast this correctly in case we write V = U + b where V is an array of shape (m,n) and b is an array of shape (n,).

For the backpropagation pass we have:

\[\pfrac{\ell}{U} = \pfrac{\ell}{V}.\]

For the derivative of \(\ell\) with respect to parameter vector \(\v b\) we have to sum all \(\prt\ell/\prt \v b = \prt\ell / \prt \v v\ls i\) for all examples in the batch:

\[\pfrac{\ell}{\v b} = \sum_{i=1}^{m} \pfrac{\ell}{\v v\ls i} = \pfrac{\ell}{V}\T \v 1\]

where \(\v 1\) is a vector with all elements equal to 1. Note that in Numpy we can simply sum over all columns in array \(V\).