\(\newcommand{\in}{\text{in}}\) \(\newcommand{\out}{\text{out}}\) \(\newcommand{\prt}{\partial}\)

6.4.3.1. Linear Block

The computational graph of a fully connected linear module is depicted in the figure below.

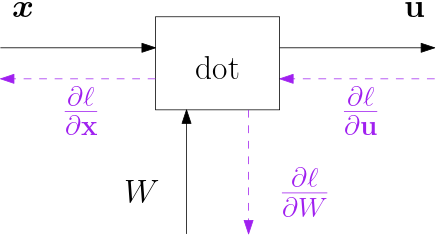
Fig. 6.4.15 Fully Connected Linear Block. The input vector \(\v x\) is mapped on output vector \(\v u = W\v x\).

The input is an \(s_\in\)-dimensional vector \(\v x\) and the output is a vector \(\v u\) that is \(s_\out\) dimensional. We have:

\[\underbrace{\v u}_{(s_\out\times 1)} = \underbrace{W}_{(s_\out\times s_\in)} \underbrace{\v x}_{(s_\in\times1)}\]

where \(W\) is an $s_\out\times s_\in$ matrix. Assuming \(\pfrac{\ell}{\v y}\) is known we can calculate \(\pfrac{\ell}{\v x}\):

\[\begin{split}\frac{\prt\ell}{\prt\v x} &= \frac{\prt \v u}{\prt\v x}\frac{\prt \ell}{\prt\v u}\\ &= W\T \frac{\prt\ell}{\prt\v u}\end{split}\]

The proof of this result is rather simple. We could either dive into matrix calculus (see Matrix Calculus) or we can give a straightforward proof by looking at the components of the vectors keeping in mind the chain rule for multivariate functions (see Multivariate Functions). We will follow the second route.

\[\begin{split}\pfrac{\ell}{x_i} &= \sum_{j=1}^{s_\out} \pfrac{u_j}{x_i}\pfrac{\ell}{u_j}\\ &= \sum_{j=1}^{s_\out} W_{ji}\pfrac{\ell}{u_j}\\ &= \sum_{j=1}^{s_\out} (W\T)_{ij} \pfrac{\ell}{u_j}\end{split}\]

and thus

\[\pfrac{\ell}{\v x} = W\T \pfrac{\ell}{\v u}\]

Next we need to know the derivative \(\prt\ell/\prt W\) in order to update the weights in a gradient descent procedure. Again we start with an elementwise analysis:

\[\pfrac{\ell}{ W_{ij}} = \sum_{k=1}^{s_\out} \pfrac{u_k}{W_{ij}} \pfrac{\ell}{u_k}\]

where

\[\begin{split}\pfrac{u_k}{W_{ij}} = \pfrac{}{W_{ij}} \sum_{l=1}^{s_in} W_{kl} x_l = \begin{cases}x_j &: i=k\\0 &: i\not=k\end{cases} = x_j \delta_{ik}\end{split}\]

substituting this into the expression for \(\prt \ell/\prt W_{ij}\) we get:

\[\pfrac{\ell}{W_{ij}} = \sum_{k=1}^{s_\out} x_j \delta_{ik} \pfrac{\ell}{u_k} = x_j \pfrac{\ell}{u_i}\]

or equivalently:

\[\pfrac{\ell}{W} = \pfrac{\ell}{\v u} \v x\T\]

Let \(X\) be the data matrix in which each row is an input vector and \(U\) is the matrix in which each row it the corresponding output vector then

\[U\T = W X\T\]

or

\[U = X W\T\]

where each row in \(U\) is the linear response to the corresponding row in \(X\). In this case:

\[\pfrac{\ell}{X\T} = W\T \pfrac{\ell}{U\T}\]

or

\[\pfrac{\ell}{X} = \pfrac{\ell}{U} W\]

For the derivative with respect to the weight matrix we have:

\[\pfrac{\ell}{W} = \left(\pfrac{\ell}{U}\right)^\top X\]