6.4.3.6. Fully Connected Neural Network

Below you find the graph for one layer but this time we use indexed symbols for the variables to make it easier to come up with an algorithm for the entire network.

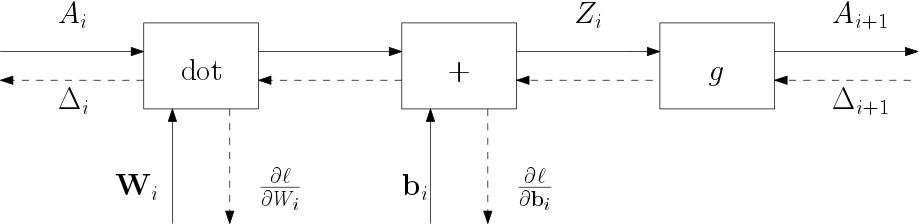
Fig. 6.4.21 One layer in a fully connected neural network.

The first layer has index \(i=0\) (to make Python coding adhere to the formules) and thus

\[A_0 = X\]

where \(X\) is the input (batch) for the network. The shape of \(X\) is \((m,n)\) where \(m\) is the number of samples in the batch and \(n\) is the number of features. The forward pass going from \(A_i\) to \(A_{i+1}\) is given by:

\[\begin{split}Z_i &= A_i W\T + \v 1 \v b_i\T\\ A_{i+1} &= g\aew(Z_i)\end{split}\]

Python code for the forward pass in the entire network is easy (assuming all arrays are properly initialized).

A[0] = X
for i in range(L):
    Z[i] = A[i] @ W[i].T + b[i]
    A[i+1] = g(Z[i])
return(A[i+1])

The backward pass is not too difficult either. First in formula’s:

\[\begin{split}\Delta_{L-1} &= (A_{L-1} - Y)/m\\ \Delta_{i} &= (g'\aew(Z_i) \odot \Delta_{i+1}) W\end{split}\]

where \(Y\) are the target vectors collected in a matrix. In Python this is something like:

D[L-1] = (A[L-1] - Y)/m
for i in range(L-2,0,-1):
    D[i] = (g_prime(Z[i]) * D[i+1]) @ W

Note that we could have calculated D[0] too but we don’t need it in calculating the derivatives with respect to all parameters.

Calculating the derivatives with respect to the parameters is needed to make one step in a gradient descent procedure. In formula:

\[\begin{split}b_i := b_i - \alpha (g'\aew(Z_i) \odot \Delta_{i+1})\T \v 1\\ W_i := W_i - \alpha (g'\aew(Z_i) \odot \Delta_{i+1})\T A_i\end{split}\]

and in Python:

for i in range(L):
    b[i] -= alpha * sum(g_prime(Z[i]) * D[i+1], axis=0)
    W[i] -= alpha * (g_prime(Z[i]) * D[i+1]).T @ A[i]

We leave it as an exercise to the reader to combine these code snippets into working code to train and use a fully connected neural network.

Just like in the gradient descent procedure for linear or logistic regression the parameters need to be initialized before the first step is made. Whereas for linear and logistic regression taking initial values to be the same (and zero) is. This is not true for a neural network. We refer to the literature (Andrew Ng’s coursera course has a nice explanation for this).