Galois theory

Introduction

In Galois theory we study symmetries of fields and the solutions of algebraic equations.

Using permutation groups we describe how the various roots of a polynomial are related. In this way properties of polynomials can be translated to properties of groups.

With Galois theory a number of classical questions can be resolved. For instance, one can show (and understand why!) the polynomial \[ x^5 - 4x + 2 \in {\mathbb Q}[x] \] does not have any solution in radicals (see also the Abel-Ruffini theorem). This is in sharp contrast to polynomials of degree at most \(4\) which always have a solution in radicals.

A second interesting application are the Greek construction problems. Galois theory gives answers to all classical construction questions, such as squaring the circle, doubling the cube, angle trisection, and more interestingly the construction of the regular \(N\)-gon.

Also in modern maths, Galois theory plays a central role. In 1993, Andrew Wiles proved Fermat's last (lost?) theorem, by proving that the Galois representation on the Tate module of elliptic curves are modular. The core of the proof of Wiles is the theory of Galois representations, which are essentially about Galois theory. In a bigger picture, the Langlands program predicts a relation with the field of automorphic forms. If you are interested, see here my article with Sander Dahmen about the work of Wiles and the Langlands program.

The BBC made an inspiring documentary about the work of Wiles:

Schedule

The lectures are given by Arno Kret.

The lectures are on Wednesdays, 9am in the morning. The lectures will be online, I will publish the zoom links via canvas.

The exercise sessions are given by Wouter Rienks, Ivo Kroon for the UvA students (in Dutch), and Rob de Jeu for the VU students (in English).

Exams: There will be a midterm, a final exam, and (hopefully for most not) a retake. Have a look at datanose for the precise times.

Prerequisites

Courses Algebra 1 (groups), Algebra 2 (Rings and Fields) given at the UvA, or equivalent, or be willing to read up/learn yourself a bit (see the list below).

Concepts from Algebra 1:

Groups
Examples of groups, such as \(V_4\), \(D_n\), \(S_n\), \(A_n\), \({\mathbb Z}/n{\mathbb Z}\), \(({\mathbb Z}/n{\mathbb Z})^\times\), \(GL_d({\mathbb Z}/n{\mathbb Z})\), \(({\mathbb R}_{>0},\cdot)\), \(({\mathbb C}, +)\), etc.
Morphisms, isomorphisms, automorphisms.
Subgroups, kernel and image, cosets, quotient group, normal subgroup, isomorphism theorems.
Quotient maps, commutator subgroup.
Semi-direct products.
Group actions. Orbit, stabilizer, orbit formula (orbit-stabilizer theorem).

Algebra 2:

Rings, fields (=lichamen in Dutch), polynomial rings, quotient ring.
Ideals, prime ideals, maximal ideals, Chinese remainder theorem.
Zero divisors, irreducible elements, principal ideal domains, unique factorization domains.
Ring morphisms, isomorphism theorem.
Structure of \(K(\alpha)\) if \(\alpha\) is algebraic or transcendent, finite field extensions, the degree of field extensions. (The notions in this bullet will be repeated in the lecture).
Finite fields.

Study goals

After completing this course, you are able to

Explain why there is no formula to solve the general polynomial of degree \(5\).
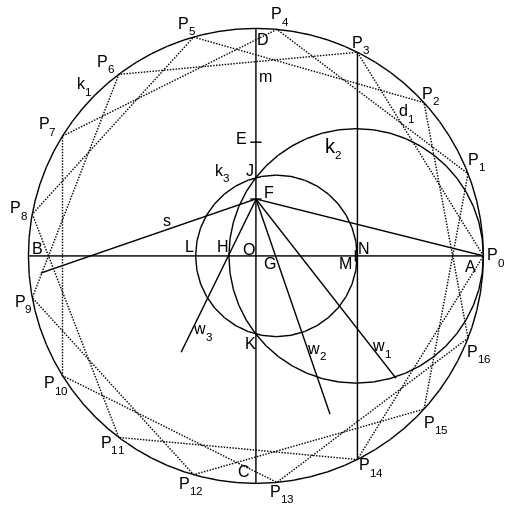
Explain and prove why it is possible to construct the regular 17-gon with ruler and compass, but it is impossible to construct the regular 19-gon.
Recognize and prove that the Galoisgroup of the polynomial \(f = X^4 - X^2 - 2 \in {\mathbb Q}[X]\) is isomorphic to Klein's 4-group.
Describe all subfields of \({\mathbb Q}(\zeta_{15})\) where \(\zeta_{15}\) is a primitive 15-th root of unity, for instance by giving for each subfield a primitive element.
Recognize and prove that the roots of the polynomial \[f = X^4 - X^3 + X^2 - X + 1 \in {\mathbb Q}[X]\] in \({\mathbb C}\) can be constructed with ruler and compass.

Literature

In the lecture we wil use the notes written by Peter Stevenhagen. These are available in Dutch and in English. For the lectures in the first two weeks, we will use chapter 14 of Stevenhagens notes, which can be found here and a translation here.

Here are number of other good lecture notes:

Books:

I would start with Stewart and Lang. I also recommend the book of Duaady, who takes a more abstract approach, which additionally contains the amazing theory of dessin d'enfants (Children drawings).

Rob de Jeu also recommendeds the book Abstract Algebra (3rd edition) by Dummit and Foote.

If you are unable to find the above books in the library, then this link contains very valuable information about the online availability of books.

Planning

Week	Material
1 and 2	Introduction and overview of the course. Symmetric polynomials. discriminant, resultant, algorithm.
3 and 4	Chapter 21: Field extensions. Algebraic and transcendent, formal adjunction of roots, algebraic closure, normal closure.
5	Chapter 22: Finite fields. The field \({\mathbb F}_{p^n}\), Frobenius, irreducible polynomials over finite fields, automorphisms of finite fields
6 and 7	Chapter 23: Separable and normal extensions. Fundamental set, perfect fields, primitive elements, normal extensions, independence of characters, norm and trace.
MIDTERM	everything from weeks 1--7
8 and 9	Chapter 24: Galoistheory. Galoisextensions, main theorem, proof of main theorem, Galoisgroup of a polynomial, cyclic extensions, cyclotomic extensions.
10 and 11	Chapter 25: Radical extensions. Construction problems, quadratic closure, radical closure, radical formulas.
12 and 13	Chapter 26: Applications of Galois theory. Main theorem of algebra, quadratic reciprocity, symmetric polynomials.
14 and 15	Open space.
FINAL Exam	everything from weeks 1-15

Beware: This planning is tentative.

Notes from the live lecture, and lecture recordings

Here you can find the notes from the live lecture. In this folder you can also download the recorded lecture for April 7th (proof of main theorem of Galois theory), the introductory lecture on Infinite Galois theory, and a video where I explain the solution to problem 3 of the midterm exam. In case you have trouble viewing the recordings, I recommend to use the VideoLAN player, available for free here.

Grading

If your final exam is \(\leq 5\), then that will be your final grade. If your exam (or retake) has grade \(\geq 5\), your final grade will be the average of exam/midterm/homework using the standard weights (60:25:15).

Homework and Exercise session

There will be homework (roughly) every week, consisting of (roughly) 2 exercises. Some exercises are worth more points than others: The ones marked with a * are worth 5 points, the others are worth 4. Your grade is the total sum of points you get.
The final homework grade is the average of all the homework grades, where we leave out the lowest 2 grades.
Hand in your homeworks before the start of the lecture of the next week (so hand in on Wednesdays before 9am).
Please hand in your homework on Canvas, and use LaTeX.
The first problem of both the exam and the midterm will be a random choice of one of the problems that was treated in the homework and the exercise session.

Here is the homework with deadlines:

Deadline
Wed Feb 3rd	No homework.
Wed Feb 10th	No homework.
Wed Feb 17th	Two problems from 15, 16, 19, 20 (Stevenhagens notes chapter 14). BEWARE: You cannot hand in both problem 15 and 16 (as pb 15 is a special case of pb 16).
Wed Feb 24th	Two problems from 18,19,29,30 (Chapter 21).
Wed Mar 3th	Two problems from 15, 32, 36, 38 (Chapter 21).
Wed Mar 10th	Two problems from 35* (Chapter 21). 7,8, 13* (Chapter 22).
Wed Mar 17th	Two problems from 17, 19, 30, 31 (Chapter 22).
Wed Mar 24th	No homework.
Wed Apr 7th	Two problems from 19, 20, 37 (Chapter 23), 16 (Chapter 24).
Wed Apr 14th	Two problems from 4, 15, 20,22 (Chapter 24).
Wed Apr 21th	Two problems from 24, 25, 29, 41 (Chapter 24). BEWARE: You cannot hand in both problem 24 and problem 25.
Wed Apr 28th	Two problems from 28, 35, 37, 53 (Chapter 24).
Wed May 12th	Two problems from 15, 17, 24, 28 (Chapter 25).

Here are the problems for the exercise session:

Week	Exercise Session Problems
5	10, 21, 23, 22 from Chapter 14
6	14, 17, 24 from Chapter 14
7	23, 24, 26 from Chapter 21. In problem 26, also prove that the group \(G = {Aut}_{{\mathbb Q}}(M)\) is isomorphic to \(V_4\), and that \(f^\alpha_{\mathbb Q} = \prod_{\sigma \in G} X - \sigma(\alpha) \in {\mathbb Q}[X]\).
8	28, 31, 37 from Chapter 21.
9	6, 11, 12, 15 from Chapter 22.
10	16, 4, 24 from Chapter 22. Also prove the following statement: Let \(K\) be a field, \(\overline K/K\) an algebraic closure and \(f \in K[X]\) a non-constant polynomial. Then \(f\) has no repeated roots in \(\overline K\) ( \(f\) is separable) if and only if \(f\) is coprime to \(f'\). [This corrects something I said in the lecture: I mistakenly made a comment that this equivalence only holds in case \(f\) is irreducible.]
11	Midterm of last year.
12	No exercise session.
13	Determine the Galois group of the extension \({\mathbb Q}(\sqrt 2, \sqrt 3)/{\mathbb Q}\). Problem 26 of chapter 23, also determine the Galois groups of the splitting fields of the listed polynomials (the last one is more difficult).
14	Problems 2,3,14 and 19 from Chapter 24.
15	Problems 23, 26, 40, 45 from Chapter 24.
16	Problems 38, 46, from Chapter 24, and the following problem: Write \(H\) for the set of \(2\times 2\)-matrices of the form \(\left( \begin{smallmatrix} a & b \cr 0 & 1 \end{smallmatrix} \right)\) with \(a \in {\mathbb F}_5^\times\) and \(b \in {\mathbb F}_5\). (a) Prove that \(H\) is a group under matrix multiplication. (b) Let \(f = X^5 - 2 \in {\mathbb Q}[X]\). Prove that Gal\((f) \cong H\). (cf. Problem 51, 52 of Chapter 24, the group \(H\) is called Aff\(({\mathbb Z}/5{\mathbb Z})\) there).
17	Problems 22, 23, 29 from Chapter 25.

(all problems are from Stevenhagens notes. Available here: Dutch, English. Chapter 14: Dutch and English)

Midterm

The midterm will be about the material from the first 7 weeks (up to and including Chapter 23, section on primitive elements). It will consist of 4 questions, and has the following structure:

Exercise 1: A two part question, where I ask you to repeat one of the statements of a theorem or definition from the notes. Second part the proof of one of the following results: 21.3, 21.5, 21.9, 22.1, 22.10, 23.1, 23.5, 23.6.
Exercise 2: An arbitrary choice from the problems treated in homework and the exercise sessions.
Exercise 3 and 4: Further test your understanding of the subject.

Midterm of last year, two years ago and three years ago.

Misha's translation of the midterm of two years ago.

Exam

The exam will be about Chapter 21-25 (page 74) and the hand out on symmetric polynomials.

The final exam will consist of 5 questions, and have the following structure:

Exercise 1: An exercise with two parts, where I test if you are able to formulate a theorem and or a definition, and if you know the proof of the theorem. Be aware: I expect that you know the statements of all definitions, all theorems/propositions/lemmas. Of the following results I expect that you will also know the proof:

21.3, 21.5, 21.9, 22.10, 23.1, 23.6, 23.14, 24.3, 24.6, 24.7, 24.9, and 25.17

If you use the english version of the notes, you should study the following list: 21.3, 21.5, 21.9, 22.10, 23.1, 23.6, 23.14, 24.3, 24.7, 24.8, 24.10, and 25.17, which is almost identical, except for a couple of numbers in section 24. In one of the two versions there is no theorem/proposition/lemma with number 24.6.

Exercise 2: An arbitrary choice from the problems that are treated in the exercise session or in the homework.
Exercises 3 to 5: Further test of knowledge and understanding, see also midterm and exam of last year.

Here are a couple of exams from prior years:

2019/2020: The midterm, exam and retake.
2018/2019: The midterm, exam and retake.
2017/2018: The midterm, exam and retake.
2016/2017: The exam and retake.

A number of other things:

The exam is a closed book exam with online surveillance. Please also have a close look at the zoom protocol for taking online exams at the UvA.

Fraud

Fraud will be reported, see here for the guidelines.

You are allowed to make homework together with your fellow students and think about solutions using WhatsApp/Internet/whatever. In no circumstance copying is allowed : You always have to write your own solutions.

Also sharing your own homework through "whatever" is not allowed, and will be reported as fraud.

When you hand in homework, you declare that you understand and are capable to explain what you have written. If the assistant has the impression that your solution was copied, he or she may ask you to explain your solution. If you are not able to do this properly, we may decide that your homework was fraud.

Honours: Infinite Galois theory (optional)

Students with grade at least 7.5 for the midterm can participate in the honours program. This extension is worth 3 additional EC credit points. The course is mostly self-study.

For the date of the exam, see datanose. Most of the work will be to solve and work out a long list of homework problems. You have to work these out in LaTex and hand in before the day of the final exam of the honours extension.

The extension is about infinite Galois theory. We will study field extensions that are algebraic but not necessarily finite. In this context we can also define what normal and separable extensions are. A typical example of such an extension is the algebraic closure of a field, which are usually of infinite degree (otherwise of degree at most \(2\)).

Literature to read: Lecture notes of Hendrik Lenstra 'Galois theory for schemes' (chapter 1 and 2 about profinite groups and infinite Galois theory for fields). Your grade will be based on your written homework, and the final exam.

Homework. Do exercises: 1.8, 1.9, 1.14, 1.16, 2.13, 2.14, 2.16 en 2.17. Additionally: At least 8 exercises from Chapter 1 and 2. Write the homework in LaTeX. Solving more difficult problems will lead to a higher grade.

Exam. A random choice from the homework problems. Additionally, study the text on infinite Galois theory (do not have to study the part on schemes!).

Math Doctor Bob (optional)

For an abstract course such as Galois theory it is crucial to know a lot of examples. See also my exams, in the more difficult questions I often ask students to come up with their own examples.

Here are a number of nice examples discussed:

Galois Correspondence 1 - Examples

Cyclotomic Polynomials

Example: Quartic Extension

Example of Splitting field

Youtube-lectures of Benedict Gross (optional)

For if you want more: "Abstract algebra" of Benedict Gross.

Two interesting lectures of Jean-Pierre Serre (optional)

A lecture on finite groups and the relation with Galois groups, a second video on abelian Galois groups.

Mathematics Stackexchange (optional)

Stackexchange is a good website where you can go with all your questions on Galois theory:

Pari (optional)

Pari is a free computer program that you can use to calculate all sorts of things. For instance Galois groups. It is a free program that you can get here. Some Pari examples:

Calculate the Galois group of the polynomials \(X^5 - X + 1\) and \(X^4 + X^3 + X^2 + X + 1 \in {\mathbb Q}[X]\):

gp > polgalois(x^5-x+1)
%1 = [120, -1, 1, "S5"]
gp > polgalois(x^4+x^3+x^2+x+1)
%2 = [4, -1, 1, "C(4) = 4"]

Compute \(2^{123}\) modulo \(456\):

gp > Mod(2^123,456)
%3 = Mod(392, 456)

Determine the prime factorization of the discriminant of the polynomial \(X^5 + X^2 - X + 1 \in {\mathbb Q}[X]\):

gp > factor(poldisc(x^5+x^2-x+1))
%4 =
[ 2 2]
[ 5 2]
[23 1]

Factor the seventh cyclotomic polynomial \[ \Phi_7 = X^6 + X^5 + X^4 + X^3 + X^2 + X + 1 \in {\mathbb Z}[X] \] over \({\mathbb Q}\) and then over \({\mathbb F}_7\):

gp > f = x^6+x^5+x^4+x^3+x^2+x+1
%5 = x^6 + x^5 + x^4 + x^3 + x^2 + x + 1
gp > factor(f)
%6 = [x^6 + x^5 + x^4 + x^3 + x^2 + x + 1 1]
gp > factor(f*Mod(1,7))
%7 =
[Mod(1, 7)*x + Mod(6, 7) 6]

After some thought, you see that the answer with label ''\(\%7\)'' is equivalent to \[ \Phi_7 = (X-1)^6 \in {\mathbb F}_7[X]. \]

Here a list with all Pari instructions: