5. Local Operators

Local operators are the most important operators in image processing. To calculate the value in one point \(\v x\) in the output image a local operator looks at all values in a, usually small, neighborhood \(\set N(\v x)\) of that point in the input image.

A simple example is local average filter. We take \(\set N(\v x) = \{\v y \bigm| \|\v y-\v x\| \leq R\}\) that is all points with distance less then or equal \(R\) to \(\v x\). The function \(t\) in this case takes the average value of all \(f(\v y)\) within the neighborhood of \(\v x\) and assigns the average to \(g(\v x)\).

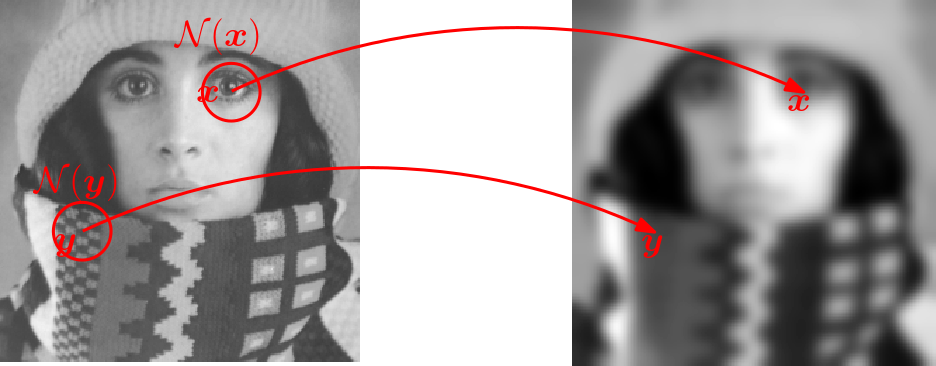
../../../_images/loc_nbh.png

Fig. 5.1 Local Operator. For all \(\v x\) in the domain of image \(f\) the (weighted) mean value in \(\set N(\v x)\) is calculated and assigned to \(g(\v x)\).

For an image defined on a continuous domain the average is an integration, for a discrete (sampled) image the average is a summation.

The definition given above for a local operator encompasses almost everything that you might think of. But as often in science the power of a theory is based on restricting the possibilities. In this chapter we will consider:

  • Translation Invariant Operators. For these operators the exact position of the neighborhood in the image is irrelevant. The neighborhood of a point \(\v x_1\) is a translated version of the neighborhood of a point \(\v x_2\). Let \(\set N\) denote some subset of the domain of the image (most often centred at and containing the origin) then for a translation invariant operator \(\set N(\v x) = \set N+\v x\) where \(\set N +\v x\) is the translation of \(\set N\) over vector \(\v x\).

    Translation invariance is the mathematical way to express that we would like to treat every point in the image domain in the same way. I.e. we are looking for homogeneous image operators.

Furthermore we will consider the classes of linear and morphological operators.

  • Linear Operators. A linear operator is an operator \(\op T\) such that for all images \(f\) and \(g\) and constants \(\alpha\) and \(\beta\):

    \[\op T( \alpha f + \beta g) = \alpha \op T f + \beta \op T g\]

    We say that a linear operator distributes over a weighted sum of images.

  • Morphological Operators. There are two basic types of morphological operators: erosions and dilations. An erosion is an operator that distributes over a pointwise minimum of images (denoted with \(\wedge\)):

    \[\op E ( (\alpha + f) \wedge (\beta + g) ) = (\alpha + \op E f) \wedge (\beta + \op E g)\]

    A dilation \(\op D\) is defined as an operator that distributes over a pointwise maximum of images:

    \[\op D ( (\alpha + f) \vee (\beta + g) ) = (\alpha + \op D f) \vee (\beta + \op D g)\]

    Observe that weighting for morphological images is additive whereas for linear operators weighting is multiplicative.

For both these classes a lot of theory is available. In these lecture notes we only give a very brief introduction to both types of operators.

And of course a lot of local operators that are neither purely linear or purely morphological are being used in image processing. In this chapter we only give a few examples: the percentile filter and the bilateral filter.