5.2.4. Kirchhoffs Laws¶

Networks (circuits) of electronic components (for now we only consider resistors) can be quite complex. E.g. consider the circuit below:

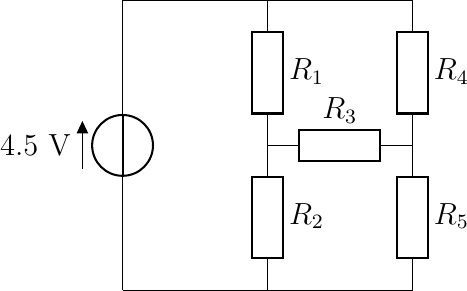
Figure made with TikZ

There is one battery of 4.5 V in the circuit and because of this currents will start to flow. In the stable situation we have stable voltages across all components and stable currents through all components.

To calculate all voltages and currents all we need is Ohm’s law and Kirchhoffs laws. Ohm’s law relates the voltage across a component with the current through the component:

\[U = I\; R\]

Kirchhoffs laws are quite simple. In fact we have used them implicitly when we considered serial and parallel circuits of resistors.

5.2.4.1. Kirchhoff’s Current Law¶

At any node in a circuit the sum of currents flowing into that node is equal to the sum of currents flowing out of that node.

In case we treat currents as positive or negative to indicate the direction of the current, KCL becomes really simple:

\[\sum_k I_k = 0\]

i.e. the sum of all currents leading into one node is zero.

5.2.4.2. Kirchhoff Voltage Law¶

The directed sum of electrical potential differences (voltages) around any closed network is zero:

\[\sum_k U_k = 0\]