5.2.3. Parallel Circuits

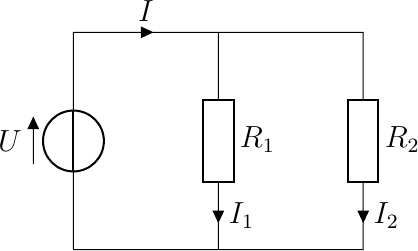
Figure made with TikZ

Fig. 5.9 Circuit with two resistors in parallel

Consider a circuit with two resistors in parallel. It is a closed circuit and current will flow. The voltage drop over both resistors is the same and equal to the battery voltage \(U\). Using Ohm’s law we then can calculate the current flowing through the resistors:

\[\begin{split}I_1 = \frac{U}{R_1}\\ I_2 = \frac{U}{R_2}\end{split}\]

The total current flowing from the battery through the circuit is the sum of \(I_1\) and \(I_2\):

\[I = I_1 + I_2 = \frac{U}{R_1} + \frac{U}{R_2}\]

i.e. the two resistors in parallel act as one resistor with resistance \(R\) such that

\[\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}\]

Our analysis above can be done for an arbitrary number of resistors in a parallel circuit.

In a parallel connection of resistors the voltage across all resistors is the same, the current flowing through each resistor is dependent on its resistance in relation to all other resistances.