5.2.6. Power

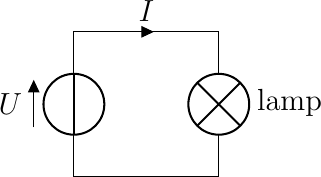
Fig. 5.11 Simple electronic circuit with a battery and a lamp

Again consider the simple circuit of a battery of voltage \(U\) and a lamp of resistance \(R\). In the closed circuit the lamp will light up. You will not only notice the light it gives but als that is getting (very) warm. In fact most electrical energy of classical light bulbs is turned into heat and not in light.

The power, that is energy per unit of time, equals:

\[P = U\, I = I^2\, R = \frac{U^2}{R}\]

If we switch from a battery to an AC power source, the voltage \(u\) and therefore current \(i\) are time dependent and so will be the dissipated power: still \(P=u\,i\). But then the power will alternate as well, at the maximal value of \(u\) it will be maximal, then it drops to zero and jumps back up. Let’s consider the 230 outlet:

\[u(t) = 325 \sin( 2\pi 50 t)\]

and a lamp of resistance \(R\). The power then is:

\[p(t) = \frac{u^2(t)}{R} = \frac{325^2}{R} \sin^2( 2\pi 50 t)\]

The power dissipation thus is fluctuating between \(0\) and \(325^2/R\). But that is not what we are often interested in. If we leave the lamp on for only a few seconds it will have gone through hundreds of complete cycles of 1/50 th of a second. We are interested in the avarage power over time intervals considerably longer then just one cycle.

By convention for an AC power source we document its effective voltage being the voltage level of a dc source with the same power dissipation.

Let’s do the calculation for a sinusoidal source (like the AC poweroutlet). The energy dissipated in a resistor of 1 ohm in 1/50 of a second is given by the integral:

\[\begin{split}E = 325^2 \int_0^{1/50} \sin^2(2\pi 50 t) dt\\ = 325^2 / 100\end{split}\]

(believe me or use Mathematica to convince yourself). The energy dissipated in 1/50 th of a second in 1 ohm resister using a DC source of \(U_\text{eff}\) volt is:

\[E = U^2_\text{eff} / 50\]

Equating these two expressions for \(E\) we get:

\[U_\text{eff} = \frac{325}{\sqrt{2}} = 230\]

Note that the factor \(\sqrt{2}\) comes from integrating a sinusoidal source. Different factors are obtained for other wave forms. You might try to calculate the effictive amplitude for a triangular wave form or for a square wave form (important when you look at the signals in digital circuits).