2.3. Linear Discrete Time Systems

We have seen that the working of any LTI system, continuous or discrete time, is completely characterized as a convolution with its impulse response.

For discrete time systems that are often implemented in software, the convolution thus seems the logical way to implement such a system (or filter as we will call it). But for discrete time systems there is another way of characterizing and implementing a class of LTI systems, namely through the use of difference equations.

Consider an input-output relation specified as:

\[a_0 y[n] + a_1 y[n-1] + \cdots + a_N y[n-N] = b_0 x[n] + b_1 x[n-1] + \cdots + b_M x[n-M]\]

or

(2.1)\[\sum_{k=0}^N a_k y[n-k] = \sum_{k=0}^M b_k x[n-k]\]

This expression for the difference equation easily leads to the conclusion that the system described is indeed an LTI system.

Setting \(a_0=1\) (which of course can be done by dividing the above expression by \(a_0\)) we can rewrite in the form:

\[y[n] = \sum_{k=0}^M b_k x[n-k] - \sum_{k=1}^N a_k y[n-k]\]

this is a recipe for calculating \(y[n]\) as a linear combination of \(x[n],\ldots,x[n-M]\) and of \(y[n-1],\ldots,y[n-N]\). I.e. to calculate \(y[n]\) we use values of the input signal but also of the output signal that we have already calculated.

Consider the following example:

\[y[n] = x[n] + \alpha y[n-1]\]

Because the difference equation described an LTI system, it should also be characterized with its impulse response funtion \(h[n]\). Note that \(h[n]\) is the response \(y[n]\) given the impulse as input \(x[n]=\delta[n]\).

Assuming \(y[-1]=0\) we get:

\[\begin{split}h[0] &= 1\\ h[1] &= \alpha\\ h[2] &= \alpha^2\\ \vdots\\ h[n] &= \alpha^n\end{split}\]

Note that the impulse response is non zero for all \(n\geq 0\). This is called an infinite impulse response filter. Evidently this filter is only stable in case \(|\alpha|<1\).

Show code for figure
1import numpy as np
2import matplotlib.pyplot as plt
3
4plt.clf()
5n = np.arange(32)
6h = 0.8**n
7plt.stem(n, h, use_line_collection=True);
8
9plt.savefig('source/figures/iir_simple_1.png')
../_images/iir_simple_1.png

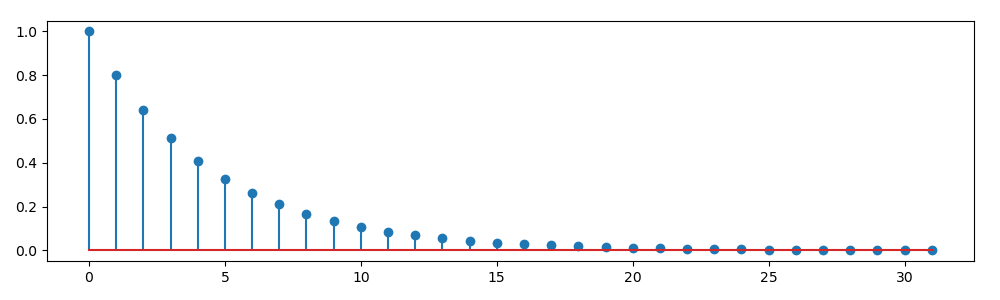
Fig. 2.10 Infinite impulse response: \(h[n]=0.8^n u[n]\)

For a negative value for \(\alpha\) we get a totally different linear system.

Show code for figure
1plt.clf()
2n = np.arange(32)
3h = (-0.8)**n
4plt.stem(n, h, use_line_collection=True);
5
6plt.savefig('source/figures/iir_simple_2.png')
../_images/iir_simple_2.png

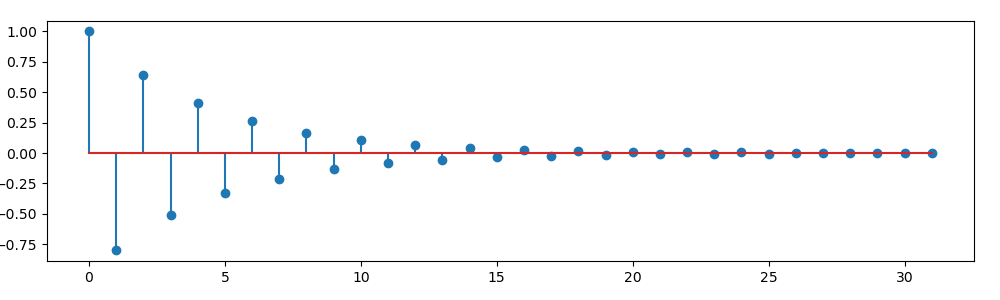
Fig. 2.11 Infinite impulse response: \(h[n]=(-0.8)^n u[n]\)

In this section we won’t look at these IIR filters but come back to this subject in the section of filters after we have discussed the Z-transform.