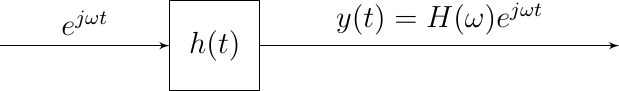2.4. Eigenfunctions

A remarkable fact of linear systems is that the complex exponentials are eigenfunctions of a linear system. I.e. if we take a complex exponential \(x(t)=\exp(j\omega t)\) as input, the output is a complex exponential, with the same frequency as the input but multiplied with a complex constant (dependent on the frequency).

Figure made with TikZ

Fig. 2.12 Complex Exponentials are the Eigenfunctions of a CT LTI Linear System

Consider the system with impulse response \(h\) then the output is given by:

\[y(t) = \int_{-\infty}^{\infty} e^{j\omega(t-u)} h(u) du\]

We can simplify this as

\[y(t) = e^{j \omega t} \int_{-\infty}^{\infty} e^{-j\omega u} h(u) du\]

Observe that the integral only depends on \(\omega\) and we denote it as \(H(\omega)\), then:

\[y(t) = e^{j \omega t} H(\omega)\]

i.e. in case the input of a linear system is a sinusoidal signal (complex exponential) the output is the exponential function (sinusoidal function with the same frequency) multiplied with a complex factor \(H(\omega)\) that is completely characterized by the linear system (its impulse response).

The function \(H\)

(2.2)\[H(\omega) = \int_{-\infty}^{\infty} e^{-j\omega u} h(u) du\]

is called the Fourier transform of \(h\). The Fourier transform will play a major role in this lecture series.

Let’s redo this analysis for a real valued function: \(x(t)=\cos(\w t)\). We know that

\[x(t) = \cos(\w t) = \half (e^{j\w t} + e^{-j\w t})\]

Because we are considering a linear system we have:

\[\begin{split}y(t) &= (\op Lx)(t) = \half( \op L(e^{j\w t}) + \op L(e^{-j\w t}) )\\ &= \half\left( H(\w)e^{j\w t} + H(-\w) e^{-j\w t} \right)\end{split}\]

Note that from the definition of the Fourier transform (Eq. (2.2))we can see that if \(h\) is real valued function (which in practice it always is) that \(H(-\w) = H^\star(\w)\). Writing \(H(\w)\) in polar notation:

\[\begin{split}H(\w) &= |H(\w)| e^{j\angle H(\w)}\\ H(-\w) &= H^\star(\w) = |H(\w)| e^{-j\angle H(\w)}\end{split}\]

So

\[\begin{split}y(t) &= \half |H(\w)| \left( e^{j(\w t+\angle H(\w)} + e^{-j(\w t +\angle H(\w)} \right)\\ &= |H(\w)| \cos( \w t + \angle H(\w))\end{split}\]

So for a linear system with impulse response \(h\) we have

\[x(t) = e^{j\w t} \quad\xrightarrow{\quad L\quad}\quad y(t) = H(\w) e^{j\w t}\]

and

\[x(t) = \cos(\w t) \quad\xrightarrow{\quad L\quad}\quad y(t) = |H(w)| \cos( \w t + \angle H(\w))\]

Evidently the use of complex exponential functions allows for a much more convenient (and short) notation. Complex numbers are really indispensible in signal processing theory.