IIR Filters

Infinite impulse response filters are characterized with a difference equation like:

\[y[n] = \sum_{k=0}^M b_k x[n-k] - \sum_{k=1}^N a_k y[n-k]\]

as discussed in the second chapter on LTI systems. There we have shown that for instance a simple system characterized with

\[y[n] = x[n] + \alpha y[n-1]\]

corresponds with an LTI system with an infinite impulse response:

\[h[n] = (1\;\alpha\;\alpha^2\;\alpha^3\;\cdots)\]

and we have established that it is a stable filter in case \(|\alpha|<1\). In this section we will analyze these IIR filters in the Z-domain.

Setting \(a_0=1\) the difference equation at the top can be rewritten as:

\[\sum_{k=0}^N a_k y[n-k] = \sum_{k=0}^M b_k x[n-k]\]

Applying the Z-transform to both sides (and using the shift property) we get

\[\left(\sum_{k=0}^N a_k z^{-k} \right) Y(z) = \left(\sum_{k=0}^M b_k z^{-k} \right) X(z)\]

or

\[H(z) = \frac{Y(z)}{X(z)} = \frac{\sum_{k=0}^M b_k z^{-k}}{\sum_{k=0}^N a_k z^{-k}}\]

In these notes we are going to restrict ourselves to the case \(M\leq 2\) and \(N\leq2\). In audio processing such a digital filter is called a biquad filter.

\[\begin{split}H(z) &= \frac{b_0 + b_1 z^{-1} + b_2 z^{-2}}{a_0 + a_1 z^{-1} + a_2 z^{-2}}\\ &= \frac{b_0 z^2 + b_1 z + b_2}{a_0 z^2 + a_1 z + a_2}\end{split}\]

The first expression if the starting point to represent the filter as a block diagram. The second form is starting point for poles-zeros analysis of the filter.

The analysis in the Z-domain is done through some examples of digital filters. Consider the filter defined with difference equation

\[y[n] = \alpha y[n-1] + b_0 x[n]\]

Leading to the transfer function \(H(z)\):

\[\begin{split}H(z) = \frac{Y(z)}{X(z)} &= \frac{b_0}{1-\alpha z^{-1}}\\ &=\frac{b_0 z}{z-\alpha}\end{split}\]

The pole of this filter is at \(z=\alpha\) and thus the filter is stable for \(\alpha<1\).

The frequency response of the filter can be found by substituting \(e^{j\W}\) for \(z\) in the transfer function:

\[H(\W) = H(z)\bigg\rvert_{z=e^{j\W}} = \frac{b_0}{1-\alpha e^{-j\W}}\]
Show code for figure
1import numpy as np
2import matplotlib.pyplot as plt
3from audiolazy import z
4
5Hlow = 1/(1-0.8*z**(-1))
6Hlow.plot(freq_scale='log', rate=44100)
7plt.savefig('source/figures/lowpassresppnse.png')
../../_images/lowpassresppnse.png

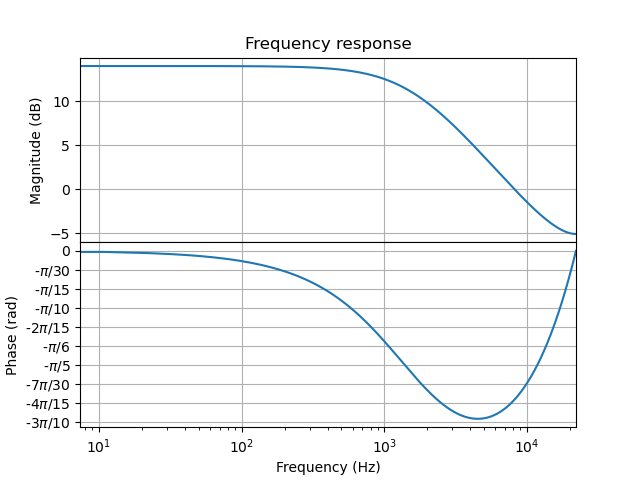
Lowpass Response of Filter with transfer function \(H(z) = \frac{1}{1-0.8 z^{-1}}\)