Bodeplots in Python

DIY Python

Consider the (angular) frequency reponse function of a low-pass filter:

$$H(\w) = \frac{1}{1+j \frac{\w}{\w_c}}$$

where $\omega_c$ is the cut-off frequency. In a Bode magnitude plot we plot the magnitude (in decibels) of the transfer function (frequency response), i.e.

$$\begin{split}20 \log | H(\omega) | = 20 \log \frac{1}{|1+j \omega / \omega_c|}\\ = - 20 \log |1+j \omega / \omega_c|\\ = - 10 \log\left( 1 + \frac{\omega^2}{\omega_c^2} \right)\end{split}$$

Be sure you can do these steps yourself, especcially the last step is not trivial!

Most often in plots we plot ‘real’ frequencies and not angular frequencies. Remember that $\omega = 2\pi f$. The cut-off frequency is taken at 2KHz leading to $\omega_c = 4000\pi$. We may write a simple python function to represent the transfer function:

In [1]: from pylab import *

In [2]: def H(w):
   ...:     wc = 4000*pi
   ...:     return 1.0 / (1.0 + 1j * w / wc)
   ...: 

and then plot it:

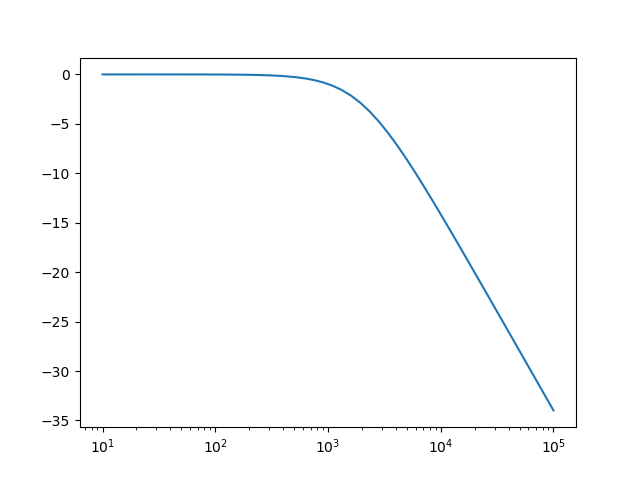
In [3]: f = logspace(1,5) # frequencies from 10**1 to 10**5

In [4]: plot(f, 20*log10(abs(H(2*pi*f)))); xscale('log')

Observe that the corner (or cut-off) frequency is at around 2000 kHz and that the decay above that frequency is 20 dB per decade (equal to 6 dB per octave).

Scipy Signal Processing Package

Scipy also contains functions to represent continuous time linear systems. An LTI system is specified in the $s$-domain. For the low-pass filter we have used in the previous section the transfer function is:

$$H(s) = \frac{1}{\frac{1}{\omega_c}s + 1}$$

In [5]: from pylab import *

In [6]: from scipy import signal

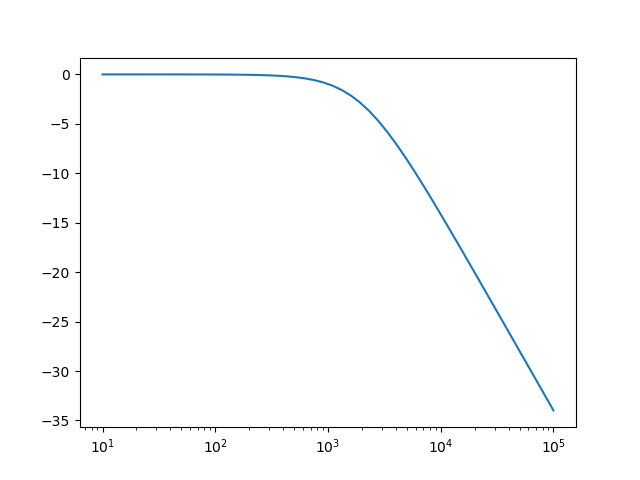
In [7]: system = signal.lti([1], [1/(4000*pi),1])

In [8]: f = logspace(1, 5)

In [9]: w = 2 * pi * f

In [10]: w, mag, phase = signal.bode(system,w)

In [11]: semilogx( f, mag);